Home, Cycles, Astrophysics, Human developmentHome, Cycles, Astrophysics, Human development 2Book of Fragapatti scienceUnmasking the anti-Oahspe of Woodson PayneShape of human head, learning and genesBackground Bio Schools Neighborhoods and WorkLogarithmic golden spiral, Fractals and unified field physicsEinstein General Relativity, Gravity and VortexDistance to Polaris (North Star)Team Kemet vs OahspeTeam Kemet vs Oahspe part 2In the Creator we TrustUp-spikes and down-spikes warm and cold yearsAfrican Slavery in AmericaWing AndersonVortex, rotation and magnetismMore studyofoahspe.com referencesPhysics equations graphics, unified field theory, strings, lines of needles, UFOsCevorkum sub-galactic vs galactic orbitVowel sign language E-O-I greetingsMartial Arts training and Oahspe teachingsThe I'hins became extinctThe Word of John 1:1 is Vortex Motion of Oahspe Book of Jehovih 1:1Biological species concept and oxygen levels of earthFaithists working for earthly Government from Ancient to KosmonMithra, Christianity, Constantine, and OahspeDifference Between an I'huan and a Ongwee-ghanThe City of Abram (Abraham)Study-of-Oahspe for the student in class and moreExosphere and Magnetosphere of the Earth's vortexAnger leads to Satan (Ego)Whatever happened to Kosmon Black?Why the I'hins in Oahspe were not albinos or dwarfsOrigin of the color and race of the I'hins, Amish, Jefferson, Faithists, questions, dependenceOahspe scientific knowledge posted on the Internet in 2005 and 1997Engaging in, aiding and abetting war and murderBig Bang, OAHSPE, Infinity, FractalsSynchronicity 111 (111.1)Oahspe related "New Concepts" and scientific confirmation on studyofoahspe.comOahspe related "New Concepts" and scientific confirmation on studyofoahspe.com part 2Oahspe related "New Concepts" and scientific confirmation on studyofoahspe.com part 3Oahspe related "New Concepts" and scientific confirmation on studyofoahspe.com part 4Oahspe related "New Concepts" and scientific confirmation on studyofoahspe.com part 5Oahspe related "New Concepts" and scientific confirmation on studyofoahspe.com part 6How accurate are the drawings in Oahspe?All-Connected, All-Person, UnityJohn Lant Original Oahspe George Van Tassel and Jim VelasquesFaithist James May Science and OahspeGeorge Washington Prophecy of AmericaCOSMOGONY by Hugh RoseScholarly Books about OahspeEtherean fire-ship toroidal propulsion systemAngels mating with physical humansBook of SaphahMore science, Astronomy, PhysicsMore science 2 Chemistry, Physics, AstronomyHigher Advanced Knowledge of OahspeOptical Network Communications - Facial recognition - Prophets - Iesu - ZodiacSun planet, Sun photosphere, Sun's stage of developmentMaya Knowledge and Oahspe, Mexicans, Puerto Ricans, Kosmon raceInstinct, DNA, hereditaryExtrasolar planets, CEVORKUM, Light speedWeather, Climate, Dark Matter, Airborne PathogensGeology - Pole-shift - Magnetic reversal - Radiometric dating-A'jiSolar-Stellar Life Cycle - End of Earth - Death, Disease, Life After DeathBiology, Primary Vortex, Life, Computing, QuantumPhysics - Light - SoundPhysics - Magnetism - GravityThe Creator - The Father- Man - Fractals - Vortex physicsHuman origins - Pygmies - I'hinsHominidae - animal-manEarly Man - Races of Man - AnthropologyOahspe vs MormonismDinosaurs, Man, fossils, early EarthReligious History, Chinvat Bridge, Archeology, RaceConfucius, Po, China, Jaffeth & Caucasian origin & destinyThe Great Pyramid of Ancient Egypt and ThothmaMathematics of Israelites and sub-Saharan Africans, CASTA SYSTEMHell, Knots, Flash devices, Riot control, use of forceBiblical flood and the sinking of PanOahspe vs Qur'anThe Constantine BibleLooeamong, Constantine, and The Roman EmpireThe Bible, Jesus, Joshu, Essenes, AnunnakiColumbus, Catholics, Conquistadors, Protestants, CrusadesQuakers and inner lightThomas PaineUS HistoryKosmon cycle, people, TECHNOLOGY, ancestry & SHALAMSubatomic particles - String Theory - Quantum - GUTMatter - Anti-Matter, Galaxies and CosmologyWalter Russell Cosmogony Einstein Fractals Cellular Automata ManichaeanHolographic CosmosAerospace engineering, space-ships, space travelSpace clouds, Earth travel, ORACHNEBUAHGALAHTables of prophecy and historyThe Beast, Pets and AnimalsORACHNEBUAHGALAH CHARTS Cycles & ProphecyAngels rank, universe, genetics, Loo'isNordic Aliens-Angels, Greys, Neoteny and ManPower of Attraction - Visualization - Spiritual gifts, energy, ceremonySpiritual message - UFOs - EthereansCosmic Consciousness, cycles, human behavior, ZodiacCycles, Predictions, Earth events, A'jiLife Development Darkness Light CyclesNebula, Earth's atmosphere, heat & cold, eclipse, prophecyTrue PropheciesPredictionsDirect Inspiration, Walter RussellMisc. vortex, matter, periodic table, solar system, fractals, pi and cMisc. 2, E=mc2, geometry, pi and alphabet codes, chemical elementsMisc. 3, Sacred mathematics, geometry, music, harmonics, cosmology, cycles, fractals, chaosMisc. 4 life and planets, E-O-IH and geometry, DNA, facial recognitionMisc. 5 human DNA, neuroscience, 9-8-5, 33, creativity, solar powerProphecy, Pan, Harvest & DNAMagnetospheres - Solar planetary vortex - 3D HologramsEther Vortex PhysicsLanguage - Symbols - Pictographs - Creator's name - Native AmericansTornados, name vs concept, flat earth theory, UV-light, sympathetic resonance, spiritsTae and facial recognition, Ham, Shem, Guatama, I'huan, Ghan racesMathematics, Reality, primary 3, E-O-IH, Cevorkum, Ethereans, face matching, DNA, Israelites, MusicOriginal Israelites and JewsIsraelites I'huans Ghans Adinkra TesseractAfrica - Ham - I'huansETHICAL TEACHINGS OF OAHSPE, Government on Earth, digital moneyAngelic star travelers, Human origins, racesAstrophysics, OpticsOAHSPE Contradictions Imperfections CultsInfants Oahspe grades heaven progressionC allele, genetics and SNPsVisitors and CommentsDonation
|
- Also see bottom page of this website titled "Misc.
3, Sacred mathematics, geometry, music, harmonics, cosmology, cycles, fractals, chaos". - most schools [in 1999] teach classical geometry
-- the study of simple shapes like circles or squares -- not fractal geometry, Eglash said.
"fractal geometry can take us into
the far reaches of high tech science, its patterns are surprisingly common in traditional African designs, and
some of its basic concepts are fundamental to African knowledge systems." -
...although fractal designs do occur outside of Africa (Celtic knots, Ukrainian eggs, and Maori
raftors have
some excellent examples), they are not everywhere. Their strong
prevalence in Africa
(and in African-influenced
southern India) is quite specific. - Page 7 of African Fractals Modern
Computing and Indigenous Design
(1999) by Ron Eglash. -
African
impact on India is found in artefacts, ancient texts, genetic foot-prints, physical
resemblance amongst populations,
cultural and linguistic similarities, gastronomic affinities,
and a common world view. It is generally
agreed today by scientists and historians that an early
migration of African population first settled the coastal areas of south India, then spread
gradually
inland ...
- OAHSPE GOD'S BOOK OF BEN CHAPTER VII:
3. I am the living mathematics; - - Rensselaer Professor Ron Eglash. Eglash, a professor in our Department of Science and Technology Studies, has made fractals a keystone in his efforts to show minority students the cultural relevance of the STEM
(science, technology, engineering and mathematics) fields.-
"African fractals are not just the result
of spontaneous intuition; in some cases they are
created under rule-bound techiniques equivalent to western mathematics." - pages 68-69 of
African
Fractals by Ron Eglash. - Mandelbrot coined the
term "fractals" for this new geometry, and it is now used in every
scientific discipline from astrophysics to zoology. - Page 15 of African Fractals
by Ron
Eglash. - Fractals are characterized
by the repetition of similar patterns at ever-diminishing scales. Fractal geometry has emerged as one of the most exciting
frontiers on the border between mathematics and information technology and can be seen in many of the swirling patterns produced
by computer graphics. It has become a new tool for modeling in biology, geology, and other natural sciences.
Anthropologists
have observed that the patterns produced in different cultures can be characterized by specific design themes. In Europe and
America, we often see cities laid out in a grid pattern of straight streets and right-angle corners. In contrast, traditional
African settlements tend to use fractal structures-circles of circles of circular dwellings, rectangular walls enclosing ever-smaller
rectangles, and streets in which broad avenues branch down to tiny footpaths with striking geometric repetition. These indigenous
fractals are not limited to architecture; their recursive patterns echo throughout many disparate African designs and knowledge
systems.
Drawing on interviews with African designers, artists, and scientists, Ron Eglash investigates fractals in African
architecture, traditional hairstyling, textiles, sculpture, painting, carving, metalwork, religion, games, practical craft,
quantitative techniques, and symbolic systems. He also examines the political and social implications of the existence of
African fractal geometry. His book makes a unique contribution to the study of mathematics, African culture, anthropology,
and computer simulations. - From the book African Fractals by Ron Eglash.
- The
fractal settlement patterns of Africa stand in sharp contrast
to the Cartesian grids of Euro-American settlements. - Page 39 of African Fractals.
- “The step-pyramids
of Mesoamerica look like concentric squares when viewed from above. But linear concentric figures are not fractals. "First they are linear layers: the distance between lines is always the
same, and thus the number of concentric circles within the larger circle is finite. The non-linear scaling of fractals requires an ever-changing distance between lines,” Page-41-African-Fractals-Ron-Egalsh:
Pages-41-42-African-Fractals-Ron-Eglash:
- Comparing the Mayan snake pattern with an African
weaving based on the cobra skin pattern (fig. 3.3b), we see
how geometric modeling of similar natural phenomena in these
two cultures results in very different representations.
The Native
American example emphasizes the Euclidean symmetry within one size frame
('size frame" because the
term "scale" is confusing in the context of snake skin). This Mayan pattern is composed
of four shapes of the same size, a four fold symmetry. But the African example emphasizes fractal
symmetry, which
is not about right/left or up/down, but rather similarity between size frames. The
African snake pattern shows diamonds within diamonds within diamonds. - Page 43
of African Fractals.
-
...but with the impressive exception
of the Pacific Northwest carvings, fractals are
almost entirely absent from Native American designs. - Page 45 of African Fractals.Below: Kwakiutl Native Americans and design. "Finally, there are three
Native American designsthat are both indigenous and fractal. The best case is the abstract figurative art of the Haida, Kwakiutl, Tlingit, and others in the Pacific
Northwest (Holm 1965). These figures, primarily carvings, have the kind of global, nonlinear
self-similarity necessary to qualify as fractals and clearly exhibit recursive scaling of up to three or four iterations." - Page 43 of African Fractals.   Above: Tlingit Native Americans and design. - Ascher (1991) has analyzed some of the algorithmic properties of Warlpiri (Pacific Islander) sand drawings. Similar structures are also found in
Africa where they are called Lusona.
But while the Lusona tend to use similar patterns at different
scales, the Warlpiri drawings tend to use different patterns at different scales. Ascher concludes that the
Warlpiri method of combining different graph movements is analogous to algebraic combinations, but the African Lusona are best described as fractals. - Page 47 of African Fractals. -
Moses was involved in the freedom of his people. -In Kosmon all people need freedom:
"Free Your Mind and Your Ass Will Follow" - 1970 by George Clinton.
What does "free
your mind and your ass will follow" mean?
"It
means change your state of thought and your actions will change as well" - Mar 22, 2017 by GrailGuardian Space Age Hustle. -
Fractal Spirituality-The Infinite Within Our
Souls.
How can a Mystery as large as the Universe find expression within the
smallness of our souls? How can we tiny beings experience the Infinite? I found a new way to think about this question when
I learned about fractal geometry. Fractals are never ending patterns, with self-similarity at all sizes.
Love this.
I did my undergraduate work in mathematics – which I fell in love with because of the fractals. The beautiful mystery
of patterns repeating themselves at scale and in unrelated contexts was a hint at making meaning of the complexity of the
universe.
https://findingourwayhome.blog/2014/05/04/fractal-spirituality-the-infinite-within-our-souls/ - "We will see
not only in Architecture, but in traditional hairstyling, textiles, sculpture, painting, carving, metalwork, in religion, games and practical craft, in quantitative techniques and symbolic systems, Africans have used the patterns and
abstract concepts of Fractal geometry." - page 7 of African fractals. - "the first time I submitted a journal article on African
fractals, one reviewer replied that Africans could not have "true" fractal geometry because they lacked the Advanced mathematical concept
of infinity ...we have already seen another example of an infinity icon in the Nankani architecture discussed in
chapter 2. There the coils of a serpent of infinite length, sculpted into
the house walls, make use of the same association between prosperity without
end, and a geometry length without end. ..And
unlike the naturally occurring shells, the packing of this infinite length
into a finite space (the Nankani describe it as "coiling
back on itself indefinitely") cannot be mistaken for mere
mimicry of nature; it is rather the artifice of fractals."
- from Ron Eglash pages 147-149 of African Fractals. - ...four of the five basic concepts of fractal geometry--scaling, self-similarity, recursion, and infinity--are all potent aspects
of African mathematics,...- Page 176 of African Fractals. - Among the Nankani people in Northern Ghana ...
-  "...an African
working with a system of mythological symbols is performing
the same cognitive operations as a European working with a system of computer code symbols." - Claude Levi-Strauss,
page 188 of African Fractals by Ron Eglash. Claude Lévi-Strauss was a French
anthropologist and ethnologist whose work was key in the development of the theory of structuralism and structural anthropology. Often known as “the “father of modern anthropology”, he revolutionized the world of social
anthropology by implementing the methods of structuralist analysis developed by Saussuro in the field of cultural relations. - cognitive operations, such as memory,
reasoning and planning. - 1/3 to 3x scaling used in African fractal architecture are harmonics of 3. Pages
4 and 8 of THE UNIFIED CYCLE THEORY (How Cycles
Dominate the Structure of the Universe and Influence Life on Earth) by Stephen J. Puetz, 2009 says "Cycles exhibit harmonics of three. Take the period of cycles, multiply by three, and the next larger cycle results [33 x 3 = 99-100]. Conversely,
take cycle...divide it's frequency by three, and
the next smaller cycle appears [33 / 3 = 11]. Oahspe Book of Cosmology and Prophecy: Chapter IX: 2. These fall under the divisor, or multiple,
3 ...corresponding to the times, 11, 33, 99,
and so on. - ...two of the most important
things about how the world works—cycles
and fractals. https://businessmirror.com.ph/cycles-and-fractals/ - - "The fact that African fractals are rarely the result of imitating natural forms helps remind us that they are not due to "primitives" living close to nature."
But even for those rare cases in which African fractals are representations of nature,
it is clearly a self-conscious abstraction, not a mimetic [mimesis] reflection." - Page 53 of African Fractals by Ron
Eglash. - - Fractal relationship of Man and Creator:
Oahspe Book of Saphah M'hak (Dark, or Degree of Golden
Chamber):
19. I: He is my Father! He is within my soul.
I am within Him, and a very member of His person. - You
just input the fractal mathematical equation (Z = Z2 + C) and through the
process of recursion and iteration nature and the universe emerges. A complex universe of order and chaos emerges from a simple
mathematical input or algorithm. Man-made objects emerge through a different
mathematics (Euclidean).
|
|
Fractal geometry has, in many ways, replaced Euclidean geometry as the new sacred geometry for the Postmodern era. sacred: connected with God. Sacred | Encyclopedia.com
https://www.quora.com/How-did-ancient-Israelites-do-math 2021 - 5 years = 2016 answered. David
Mescheloff mentions the Israelites learned math from Mesopotamia, Egypt, Babylon, Persians, and Greeks, but he doesn't mention sub-Sahara Africa and he does not mention fractals, logarithmic spirals, or the Golden Ratio. “ Israelite,
the name given to the Faithists of Egupt” - Oahspe Book of the Arc of Bon Chapter XIII:9. - [Ron] Eglash realized that many of the
fractal designs he was seeing were consciously created. "I
began to understand that this is a knowledge system". - He was a brilliant scholar, a man of profound
wisdom, an adept at occultism, and a
bound devotee of the
false Osiris...he must build a temple to Osiris,
...But first Thothma was required to drive the Faithists out of the land, and to make
slaves of those who remained. Their numbers now amounted to three millions in the land of Egypt. Thothma therefore levied
a powerful army, driving
out the Listians or Shepherd Kings with great slaughter, and enslaving the children of Abraham, the Israelites...  Above: faces of original Israelites (Arabin'ya I'huan faithists) tribe. Above: faces of original Israelites (Arabin'ya I'huan faithists) tribe. Above: Ancient Israelites in Egyptian Captivity (slavery). Above: Ancient Israelites in Egyptian Captivity (slavery). <--Nov 7, 2019 <--Nov 7, 2019they were oppressed by cruel laws and penalties,
and were forced to reveal the mathematical science
which had been preserved with them from their distant ancestors the I'hins, to whom it was committed by the angels in the first ages of mankind. Humanity was now ripe for this development, but the surrender of their secrets was a further blow to the Israelites.
Both the knowledge and the slave labour of the
Israelites were now thus impressed into the construction of the temple of Osiris,
the Great Pyramid. And the etherean dawn
in which Moses
would bring them deliverance was still five hundred years away. [2053 - 500
= 1553 B.C.E.]. - Pages 189-190 of Darkness, Dawn And Destiny (Drawn from Oahspe)
1965 by Augustine Cahill. -
Oahspe Book of Wars Against Jehovih Chapter XLIX:
2.
...Thothma, made the following laws, to wit:
4. ...And of thy arts, of measuring and working numbers, thou shalt not keep them secret longer, or thy blood be upon thee.
"measuring
and working numbers" = mathematics.
Definition of mathematics for Students. : the science
that studies and explains numbers, -
Mathematics and art are related in a variety of ways.
Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music,
dance, Thothma did not
have the mathematical knowledge of the Israelites until he forced the Israelites to REVEAL it to him.
This mathematical knowledge was lost to the Egyptian slave masters after the
death of Thothma.
The true
Israelites kept this sacred mathematical knowledge up to modern times. Above: Original-Israelites-Abraham-86% and 90% facial match. Above:
Original-Israelites-Moses-93% and 92% facial match. Above:
Original-Israelites-Moses-93% and 92% facial match. - There
is also a frequently mentioned relationship between the Great Pyramid and the number φ, ..The legend that the architect
who designed the Great Pyramid of Khufu intentionally incorporated the Golden Mean (which is this number φ) into the proportions
of that structure ... -------------------------------------------------------------------- ...there is a specific proportional ratio that is found throughout nature. This ratio is called Phi ....
This ratio is nature's most ubiquitous fractal scaling ratio and is easy to see present in plants,
animals, seashells, vortices of water
and air, and many other phenomena of Earth. It is also
present at both the atomic and galactic scales. http://cosmometry.net/phi-fractal-scaling --------------------------------- Cantor set and fractals |
| I have read that the Cantor set is considered a fractal. I am referring to the Cantor set
in which the middle third of a real line is removed recursively...think of a fractal as
some geometrical object with
scale invariance such that if you "zoom in" on the object it
will look the same/similar...a classic fractal
such as the Koch Snowflake or the Sierpinski
triangle. I do see that Cantor's set would look the same if you kept "zooming
in". If you restrict your sight to [0,13] then the picture of Cantor's set is exatly the same as it
is
in the whole [0,1]. Again, restrict to [0,1/9] and you get the same picture. I think this is
the main property of a
fractal: a picture which repeats itself.
Remove the (open) middle third of it, i.e. get (1/3, 2/3). Now remove the middle thirds of
each of the remaining intervals,i.e. get (1/9, 2/9)
and (7/9, 8/9). Continue this process ad infinitum.
The points left over form a fractal called the standard Cantor Set.
Check
out C'vorkum light-years numbers divided into 1/3 and 1/9 (Cantor
Set fractal numbers) symmetrical number parts. ----------------------------------------------------------------------- "The logarithmic spiral and the Golden Ratio go hand in hand."
- page 118 of THE GOLDEN RATIO The Story of Phi by Mario Livio, P.h.D astrophysics. 
Logarithmic spiral - Wikipedia 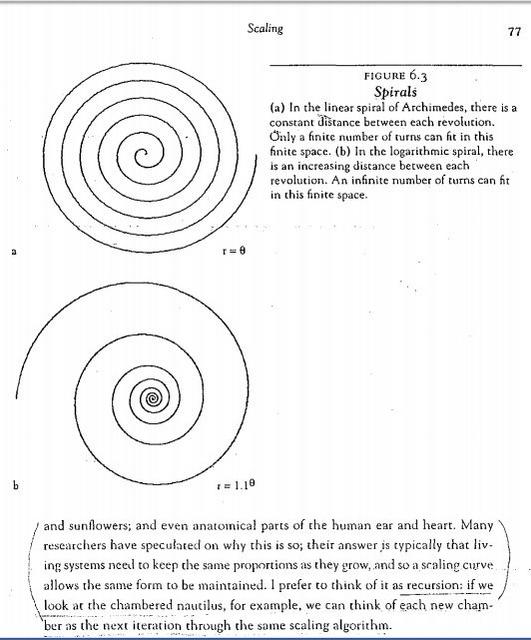
Logarithmic
spirals are fractals showing repetitive process, self-similarity, scaling, and infinity. Logarithmic Spirals
Several Ghanian
iconic figures, ...link a spiritual force with the structure
of living systems
through logarithmic spirals. - page 78 of African Fractals by Ron Eglash. ------|--galaxy-spiral---|--------------|---sub-atomic spirals---|--- Above left is Hubble Space Telescope (HST) image of NGC 4622 Spiral Galaxy. Above
right is CERN Bubble Chamber photograph of Subatomic particle tracks. Both
images above are logarithmic spirals on different scales (galactic
and subatomic). The Akan and other Ghanaian societies had a remarkable pre-colonial use of logarithmic spirals. The Akan and other Ghanaian societies had a remarkable pre-colonial use of logarithmic spirals in iconic representations for living systems. - Page 104 of African Afractals by Ron Eglash.
Oahspe Book of Wars Against Jehovih Chapter XLIX: 2. ...Thothma, made the following laws, to wit: 4.
...And of thy arts, of measuring and working numbers, thou shalt not keep them secret longer, ... Mathematics and art are related in a variety of ways.
Mathematics has itself been described
as an art motivated by beauty.
Mathematics can be discerned in arts such as music,
dance, painting, architecture, sculpture, and textiles. tex·tile.
1. any cloth
or goods produced by weaving, knitting, or felting.
Woven fabric is any
textile formed by weaving. Written [below] by -K- (akwadapa@hotmail.com) www.theakan.com February 2010. Fibonacci Numbers and the Golden Ratio in Akan weaving patterns!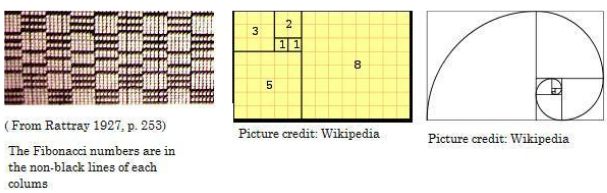 Mathematics Embedded in Akan Weaving Patterns.
Kente has become a well-known name synonymous with a certain kind of Akan and Ewe
cloth. In this article, I intend to show, perhaps for the first time, the mathematical knowledge possessed by the original inventors of this method of
weaving practised by the Akan and the Ewe.
The reader will find herein mathematical
patterns such as even and odd numbers, triangular numbers,
“Pascal's triangle” and the
binomial theorem. Most intriguing, and what certainly caught me by surprise when
I first decoded this mathematical pattern, I will show that Akan
weaving patterns embed the
so-called Fibonacci numbers from which can be obtained the golden spiral (a kind of logarithmic spiral) and from which the golden ratio is also derived. I also show other mathematical patterns which I have identified but have not yet associated with any body of known mathematics. Perhaps further research will identify
these number sequences. I also show the use of recursive triangular
and rhombus patterns
in kente cloth which suggest a certain level of fractal
encoding as well. It is remarkable that Fibonacci numbers should be found in Akan weaving patterns.
In the case of pattern [2] above, we are almost been given an approximation for the Golden Ratio, based on the numbers 8 and 13, in this case 13/8 = 1.625. Remarkable! This
is mathematics embedded in weaving patterns!

 Logarithmic
spiral overlaid on top of Sankofa. Traditional Native American and Celtic spirals are Archimedean. 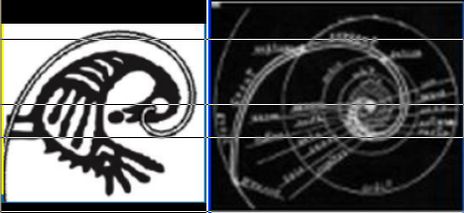  Comparison (above) of logarithmic spiral of Sankofa Adinkra and logarithmic
spiral of Oahspe plate Dissection of Great Serpent. Traditional
logarithmic spiral of Ghana Adinkra predating European explorers and logarithmic spiral of Oahspe plate are almost identical.  Above images show logarithmic spiral fractal
design in Oahspe and in computer graphics. Above images show logarithmic spiral fractal
design in Oahspe and in computer graphics.
Below are images of toroidal vortex contact structure generated as the result of Richtmyer–Meshkov instability, showing logarithmic spiral: 
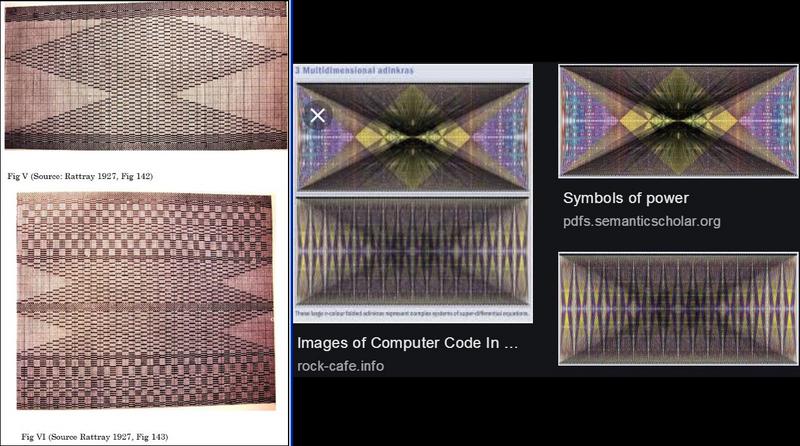 Notice
the similarities of Akan weaving patterns on Kente cloth (above on left) with mathematical codes to
visual representations of complex mathematical equations in Supersymmetry
physics (above on right and below). These Akan weaving patterns
are documented in 1927 but go back hundreds of years and
the visual representations of complex mathematical equations
in physics (Supersymmetry) date to about 2010. See Israelites I'huans Ghans
Adinkra Tesseract page of this website about 1/2 way down.  Above: Spider web geometric fractal designs.
Below: fractal architecture in Oahspe: Above: Spider web geometric fractal designs.
Below: fractal architecture in Oahspe:
OAHSPE: Book of Fragapatti CHAPTER IX:
3. Go build me an avalanza capable of carrying
three thousand million angels, with as many rooms, capable of descent and ascent, and east
and west and north and south motion, and prepare it with a magnet, that it may face to the north,
whilst traveling.
4. The builders saluted, and then withdrew, and went and built the vessel. And it was two hundred thousand paces east and
west, and the same north and south; its height was one thousand lengths, and the vesture
around it was a thousand paces thick; ... The floor was woven in copy of a spider's net, extending from the centre outward, and with circular bars at crosses; ...
-
Relative to science, fractals are essentially geometric
shapes or forms that are represented in natural objects, from a fern leaf or tree,
to a spider web ...
http://fractalarts.com/SFDA/whatarefractals.html African Fractals:
Modern Computing and Indigenous Design.
Fractals are characterized by the repetition of similar patterns
at ever-diminishing scales.
Fractal geometry has emerged
as one of the most exciting frontiers on the border between
mathematics and information technology and can be seen
in many of the swirling patterns produced
by computer graphics. It has become a new tool for modeling in biology, geology,
and other
natural sciences.
Anthropologists have observed that the patterns produced in different
cultures can be
characterized by specific design themes. In
Europe and America, we often see cities laid out in
a grid pattern of straight streets and right-angle corners. In
contrast, traditional African
settlements tend to use fractal structures-circles of circles of circular
dwellings, rectangular
walls enclosing ever-smaller rectangles, and streets in which broad avenues branch down to tiny
footpaths with striking geometric repetition. These indigenous
fractals are not limited to
architecture; their recursive patterns echo throughout many disparate African designs
and
knowledge systems. Drawing on interviews
with African designers, artists, and scientists, Ron Eglash
investigates
fractals in African architecture, traditional hairstyling, textiles, sculpture, painting,
carving,
metalwork, religion, games, practical craft, quantitative techniques, and symbolic
systems. He also examines
the political and social implications of the existence of African
fractal geometry. His book makes a unique contribution to the study of mathematics, African
culture, anthropology, and computer
simulations.
-
I buy it because I like math and geometry. I'm really fascinating by fractals applied
at design
and architecture. - Daniele De Rosa
-
I have used this book several semesters for teaching philosophy
of science, social science
methods, and Southern African political economy. It quickly demonstrates that the colonizers
understood little or nothing about 'messy, irregular'
African villages; it was Euclidean
geometry which kept them from seeing. African engineering using fractals, such as the
fractal-measured fence weave to
match the wind, is amazing. We still have very much to learn
from African peoples and this book gets Americans started
on a journey long past due. Read this
book if you want a different way of viewing the world, from hairstyles
to sculpture to urban
planning. - Carol Thompson
-
The book makes no assumptions in knowledge and will cleanly
bring in the topic of fractals in
african culture.
The concept is quite intriguing and shatters many of the held perceptions of "the hierarchy of
mathematics."
Ron Eglash is a great man and I know he loves talking with people that share
similar interests in mathematics or cybernetics.
- Lorne E. Nix
https://web.archive.org/web/20181106113150/https://www.amazon.com/African-Fractals-Modern-Computing-Indigenous/dp/0813526140
https://web.archive.org/web/20190314173707/http://homepages.rpi.edu/~eglash/eglash.dir/afractal/afractal.htm --------------------------------------------------------------------------- | Fractals are used to model soil erosion and to analyze seismic patterns as well. Seeing
that so many facets of mother nature
exhibit fractal properties, maybe the whole world around us is a fractal
after all! Actually, the most useful use
of fractals in computer science is the fractal image compression.
Why is
fractal geometry important? Fractals
help us study and understand important scientific concepts, such as the way bacteria grow,
patterns in freezing water (snowflakes) and brain waves, for example.
Their formulas have made possible many scientific breakthroughs. ...
Anything with a rhythm or pattern has a chance of being very
fractal-like.Oct 13, 2011 ...As computers get smaller and faster,
they generally produce more heat, which needs to be dissipated or else the computers will overheat and break. The smaller they are, the more this becomes a problem. Engineers at Oregon State University have developed fractal pattern that can be etched into a silicon chip
to allow a cooling fluid (such as liquid nitrogen) to uniformly flow across the surface of the chip and
keep it cool.  The fractal pattern above derived from our blood vessels provides a simple low-pressure network
to accomplish this task easily. http://fractalfoundation.org/OFC/OFC-12-2.html ... the most useful use of
fractals in computer science is the fractal image compression.
This kind of compression uses the fact that the real world is well described
by fractal geometry. By this way, images are compressed much more than by
usual ways (eg: JPEG or GIF file formats). An other advantage of fractal compression is that when
the picture is enlarged, there is no pixelisation. The picture seems very often better when its size is increased. http://kluge.in-chemnitz.de/documents/fractal/node2.html Modern medicine often involves
examining systems in the body to determine if something is malfunctioning. Since the body is full of fractals, we can use fractal math to quantify, describe, diagnose
and perhaps soon to help cure diseases. Teaching
computers to use mathematical processes to tell the difference between healthy lungs and lungs suffering from emphysema promises to help make faster, more reliable diagnoses. The fractal dimension
of the lung appears to vary between healthy and sick lungs, potentially aiding in the automated detection of the disease. 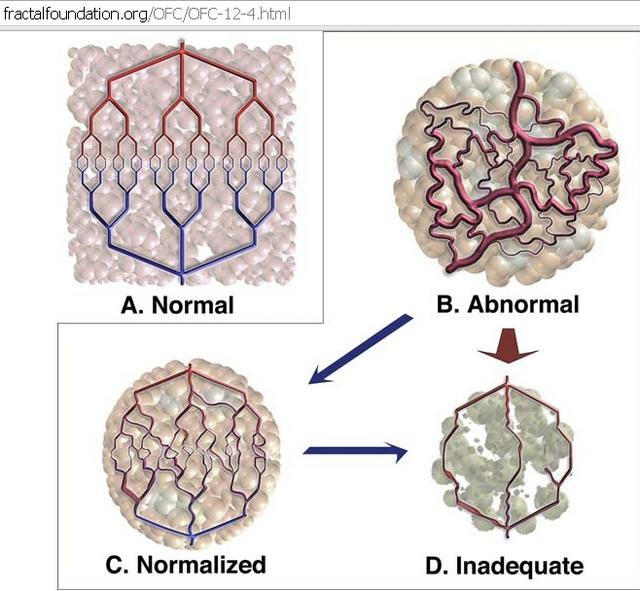 Cancer is another disease where fractal
analysis may not only help diagnose but also perhaps help treat the condition. It is well known that cancerous tumors - abnormal, rapid growth of
cells - often have a characteristic growth of new blood vessels that form a tangled mess instead of the neat,
orderly fractal network of healthy blood vessells. http://fractalfoundation.org/OFC/OFC-12-4.html The Paradigm Shattering Science of Fractals
with Dr Sab Virani, MD This work
introduces a new design approach for the use of fractal
structures for low-resistance large area transistors structures. Aspects
of layout with adapted current density and high-area utilization are considered. Furthermore the work presents a realization of
fractal structures in AlGaN/GaN technology. Both static and dynamic behaviors are characterized. The fabricated devices achieve a breakdown voltage of V BR >; 700V and on-state currents of I D =
40A at V GS = 1V. Published in: 2012
24th International Symposium on Power Semiconductor Devices and ICs https://ieeexplore.ieee.org/abstract/document/6229091 In addition to novel fractal transistors and sensors, we are developing fractals circuits for human implants and solar cells. In each case, we use the principle of biomimicry
to exploit the functionality of nature’s fractals to provide technological
advances. The fractal
circuits are ideal for bioeletronics because they mimic the neurons they are designed to stimulate and measure.
They also replicate the light-harvesting properties of fractal
trees for the solar cells. These two projects represent the most important targets for future physics research – safeguarding
human health and the Earth’s environment. For example, fractal
electronics could address neurological disorders such as Parkinson’s disease and
depression, and also improve nerve connections to prosthetic limbs. https://blogs.uoregon.edu/richardtaylor/2016/02/03/fractals-in-nanoelectronics-retinal-implants-and-solar-cells/ 
https://crimsonpublishers.com/oabb/fulltext/OABB.000541.php Cyberneticist Ron
Eglash has suggested that fractal geometry and mathematics are prevalent in African art, games, divination, trade, and architecture.
Circular houses appear in circles of circles, rectangular
houses in rectangles of rectangles, and so on. Such scaling patterns can also be found
in African textiles, sculpture, and even cornrow hairstyles.[32][82] https://en.wikipedia.org/wiki/Fractal Fractal patterns can also be found in commercially
available antennas, produced for applications such
as cellphones and wifi systems
by companies such as Fractenna in the US and Fractus in Europe.
The self-similar structure of fractal antennas
gives them the ability to receive and transmit over
a range of frequencies, allowing powerful antennas to be made more compact.  <--See similarity of Ethiopian B.C fractal crosses to cellphone fractal antenna. <--See similarity of Ethiopian B.C fractal crosses to cellphone fractal antenna.“Engineers creating
antenna for cell phones and other wireless devices need an antenna that can
have similar reception over many different
wavelengths, which means it must have a similar structure at different scales: fractals! 
“AT THE
[LEFT] IS AN ANTENNA IN A CELL PHONE BASED ON THE SIERPINSKI CARPET; AT CENTER ETCHED ON A SILICON CHIP IS THE SIERPINSKI TRIANGLE; AND
AT [RIGHT] IS OUR OLD FRIEND THE KOCH CURVE. OTHER ENGINEERING APPLICATIONS INCLUDE ARCHITECTURE, ELECTRODES, SEISMOLOGY, AND COMPUTER GRAPHICS.”
– AFRICAN FRACTALS APPLICATIONS 6: ENGINEERING FRACTALS, BY RON EGLASH I Asked Google what is Cybernetics? According
to wikipedia circular causality or feedback where the outcomes of actions
are taken as input for further actions. =
recursion, how fractals are generated. Professor
Ron Eglash who wrote African Fractals had a background in cybernetics and mathematics. Cybernetics is a transdisciplinary
and "antidisciplinary" approach concerned with regulatory and purposive systems—their structures, constraints,
and possibilities. The core concept of the discipline is circular causality or feedback—that is, where the outcomes
of actions are taken as inputs for further action. Wikipedia cy·ber·net·ics the science of communications and automatic control systems in both machines and
living things.
Above: Fulani wedding blanket (textile) showing fractal design.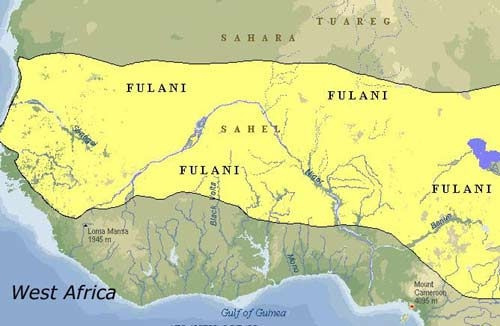  Above the Mandiack weavers
of Guinea-Bissau have also created an abstract
design... but choose to
emphasize the fractal characteristics [textile mathematical art]. Page 44 of African
Fractals.   Above is a Ashkenazi Jew with genetic (L2a1) roots in Guinea-Bissau
sub-Sahara Africa. Your mtDNA HVR1 exact matches may be recent, but they may also
be hundreds or thousands of years in the past. 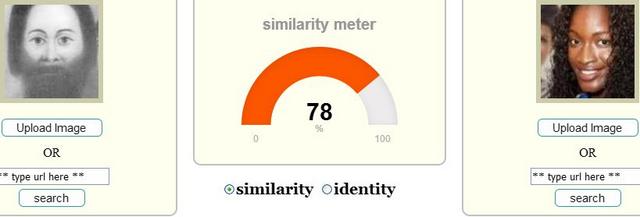 Above biometric (living mathematics)
78% facial match of pure I'huan Israelite Abraham and Sandra Araujo Miss world Guinea-Bissau 2016. 8 of the 10 top facial matches to Abraham have been African-American or sub-Saharan African. IN 1988, RON EGLASH was
studying aerial photographs of a traditional
Tanzanian village when a strangely familiar pattern caught his eye.
The thatched-roof
huts were organized in a geometric pattern of
circular clusters within circular clusters, an arrangement Eglash
recognized from his former days as a Silicon Valley computer engineer.
Stunned, Eglash digitized the images and fed the information
into a
computer. The computer's calculations agreed with his intuition: He was
seeing fractals.
Since then, Eglash has documented the use of fractal geometry-the
geometry of similar shapes repeated
on ever-shrinking scales-in
everything from hairstyles and architecture to artwork and religious
practices in
African culture. The complicated designs and surprisingly
complex mathematical processes involved in their creation may force
researchers and historians to rethink their assumptions
about
traditional African mathematics. The discovery may also provide a new
tool for teaching African-Americans about their mathematical heritage.
http://www.math.buffalo.edu/mad/special/eglash.african.fractals.html
In contrast to the relatively ordered world of Euclidean geometry
taught in most classrooms, fractal geometry yields less obvious
patterns. These patterns appear everywhere in nature, yet mathematicians
began deciphering them
only about 30 years ago.
The principles
of fractal geometry are offering scientists powerful
new tools for biomedical, geological and graphic applications.
A few
years ago, Hastings and a team of medical researchers found that the
clustering of pancreatic cells in the
human body follows the same
fractal rules that meteorologists have used to describe cloud formation
and the shapes
of snowflakes.
But Eglash envisioned a different potential for the beautiful
fractal patterns he saw
in the photos from Tanzania: a window into the
world of native cultures.
http://www.math.buffalo.edu/mad/special/eglash.african.fractals.html
Eglash had been leafing through an edited collection of research
articles on women and Third World development
when he came across an
article about a group of Tanzanian
women and their loss of autonomy in
village organization. The author blamed the women's plight on a shift
from
traditional architectural designs to a more rigid modernization
program. In the past, the women had decided where their
houses would go.
But the modernization plan ordered the village structures like a
grid-based Roman army camp, similar
to tract housing.
Eglash was just beginning a doctoral program in the history of
consciousness at the University of California at Santa Cruz. Searching
for a topic that would connect cultural issues
like race, class and
gender with technology, Eglash was intrigued by what he read and asked
the researcher to
send him pictures of the village.
After
detecting the surprising fractal patterns, Eglash began going
to museums and libraries to study aerial photographs
from other cultures
around the world.
"My assumption was that all indigenous
architecture would be more
fractal," he said. "My reasoning was that all indigenous architecture
tends
to be organized from the bottom up." This bottom-up, or
self-organized, plan contrasts with a top-down, or hierarchical,
plan in
which only a few people decide where all the houses will go.
"As it turns out, though, my reasoning was wrong," he said. "For
example,
if you look at Native American architecture, you do not see
fractals. In fact, they're quite rare." Instead, Native
American
architecture is based on a combination of circular and square symmetry,
he said.
Pueblo Bonito, an ancient ruin in northwestern New Mexico built by
the Anasazi people, consists of a big circular shape
made of connected
squares. This architectural design theme is repeated in Native American
pottery, weaving and
even folklore, said Eglash.
When Eglash looked elsewhere in the world, he saw different
geometric
design themes being used by native cultures. But he found
widespread use of fractal geometry only in Africa and southern India,
leading him to conclude that fractals
weren't a universal design theme.
Focusing on Africa, he sought to answer what property of fractals
made them so widespread in the culture.
http://www.math.buffalo.edu/mad/special/eglash.african.fractals.html
"widespread use of fractal geometry only in
Africa and southern India". Southern India is where the concept of zero (used in numerical computing) came from along
with "arabic numerals' and
the decimal system. ---
Eglash expanded on his work in
Africa after he won a Fulbright Grant in 1993.
He toured
central and western Africa, going as far north as the
Sahel, the area just south of the Sahara Desert, and as far south
as the
equator. He visited seven countries in all.
"Basically I just toured around looking for fractals, and when I
found something that had a scaling
geometry, I would ask the folks what
was going on-why they had made it that way," he said.
In many cases,
however, Eglash found that step-by-step mathematical procedures
were producing these designs, many of them surprisingly sophisticated.
Eglash realized that many
of the
fractal designs he was seeing were consciously
created. "I began to
understand that this is a knowledge system, perhaps not as formal as
western
fractal geometry but just as much a conscious use of those same
geometric concepts," he said. "As we say in California, it blew my
mind." In Senegal, Eglash learned about
a fortune-telling system that
relies on a mathematical operation reminiscent of error checks on
contemporary computer
systems.
In traditional Bamana
fortune-telling ...The mathematical operation is called addition modulo 2,
which simply gives the remainder after
division by two. But in this case, the two
"words" produced by the priest, each consisting of four odd or
even
strokes, become the input for a new round of addition modulo 2. In other
words, it's a pseudo random-number generator, the same thing computers
do when they produce random
numbers. It's also a numerical feedback
loop, just as fractals are generated by a geometric feedback loop. "Here is this absolutely astonishing numerical feedback loop, which is indigenous,"
said Eglash.
"So you can see the concepts of fractal geometry resonate throughout many facets of African
culture." Lawrence Shirley, chairman of the mathematics department at Towson (Md.) University,
lived
in Nigeria for 15 years and taught at Ahmadu Bello University in Zaria, Nigeria. He said
he's impressed with Eglash's observations of fractal geometry in Africa. "It's
amazing how he was able to pull things out of the culture and fit them into mathematics
developed in the West,"
Shirley said. "He really did see a lot of interesting new mathematics
that others had missed." Eglash said
the fractal design themes reveal that traditional African
mathematics may be much more complicated than previously
thought. Now an assistant professor of
science and technology studies at Rensselaer Polytechnic Institute in Troy,
Eglash has written
about the revelation in a new book, "African Fractals: Modern Computing and Indigenous Design."
---
Recent mathematical developments like fractal geometry
represented the top of the ladder in most
western thinking, he said. "But it's much more useful
to think about the development of
mathematics as a kind of branching structure and that what blossomed very late on
European
branches might have bloomed much earlier on the limbs of others. "When Europeans first came to Africa, they considered the architecture very disorganized and
thus primitive.
It never occurred to them that the Africans might have been using a form of
mathematics that they hadn't even discovered
yet." Eglash said educators also need to rethink
the way in which disciplines like African studies
have tended to skip over mathematics and
related areas. To remedy that oversight, Eglash said he's been working with African-American
math teachers in the United States on ways to get minorities more interested
in the subject.
Dr. Ron Eglash: Assistant Professor .
in African mathematics:
numeric systems in Africa:
Players in Ghana use the
term "marching group" for a self-replicating pattern,
such as the example
below. Here the number of counters in a series of cups each
decrease by one (e.g. 4-3-2-1).
As simple as it seems,
this concept of a self replicating pattern is at the heart of some
sophisticated mathematical concepts.
http://homepages.rpi.edu/~eglash/eglash.dir/afractal/Eglash_Odumosu.pdf
---
The valid question arises, in what ways can an
understanding of African
mathematical representations, fractals, complexity and chaos in indigenous cultural
practices assist us in theorizing about the future?
-
In our opinion, probably,the greatest point that can be taken away from our
recent research
Eglash (1999) into African mathematics is an appreciation of
African indigenous creativity
and quantitative ability. As Hull (1976) noted, large
urban centers were disregarded
by the colonialists because they did not utilize
Cartesian
typology. The complex fractal nature of these settlements went unappreciated.
This point
is crucial in any discussion of possible applications of current research.
The sheer redemptive power of knowledge is at play here. Even today, people living on the
African
continent may still think of their indigenous past as primitive and non-rational.
An understanding
of the fractal characteristics of indigenous culture enables an
appreciation of the
complexity of the ‘mundane’ indigenous artifacts. This singular
understanding can act
as a powerful motivator for rethinking modernity.
-
"Bottom-up"
social political structure of Africans vs the top-down colonial structure:
It is widely accepted in the
STS [science and technology studies] community
that indigenous
communities often posses tacit knowledge that may be invaluable
in problem solving
(Wynne 1996, Epstein 1996) but is usually deprivileged within the dominant discourse.
We have shown, for example, that many traditional African villages were structured in a
“bottom-up”
process, using self-organization rather than imposed order. Could
the top-down
hierarchal approaches that linger on in so many post-colonial African countries – often due to
the legacies of colonialism – also give way to more bottom-up self-organizing social processes?
There is an obvious need for a change in the methodologies of modernity on the African continent;
perhaps hybridizing
indigenous mathematical representations can provide fresh thinking to a
persistent problem.
http://homepages.rpi.edu/~eglash/eglash.dir/afractal/Eglash_Odumosu.pdf
- --- A discussion of the relationship between pi and the Great Pyramid of Khufu. ... we know about ancient Egyptian mathematics (based
primarily on the Rhind Papyrus), .... the mathematical
knowledge of the architect who built the Great Pyramid. It’s
possible that pi , phi or both, as we understand them today, could have been the factors in the design of the pyramid. A detail of the geometries and calculations is below: relationship of fractals to pi:
Pi
and fractal sets
The Mandelbrot set - Dave Boll - Gerald Edgar
In 1991 David Bolle tried to verify if the narrowing
we can see at (-0.75,0) was actually infinitely thin. That is to
say that that however wide a non-zero width vertical line
would be passing through that point it would
meet the fractal set before the x-axis. And
D Bolle then had the idea of using the point c=(-0.75,X) for the quadratic iteration and to make X tend to 0. And there, what was his surprise
when he counted the number of iterations before which the series diverged and by discovering the following table .: X-----iterations
1.0 3
0.1 33
0.01 315
0.001 3143
0.0001 31417
0.00001 314160
0.000001 3141593
0.0000001 31415928
Yes, it was
Pi that was appearing magnificientely ! As he could not manage to prove this he posted it in 1992 on the sci.maths newsgroup. Gerald Edgar from a university of Ohio answered it
on 27 march 1992 by bringing an intuitive explanation of this result.
This has been put lower down in the "Trial" section.
http://www.pi314.net/eng/mandelbrot.php
RonEglash Designing for Generative Justice (African fractals). At
5:44 of RonEglash youtube video Benoit Mandelbrot's (considered the father of fractal geometry in America and Europe) favorite fractal
image is the African Ba-lia village of southern Zambia. Mandelbrot had slides
from Ron Eglash's book.  At 11:45 of RonEglash youtube video cornrow hairstyles, fractals in braiding patterns made it through the middle passage of the transatlantic
slave trade. Polyrhythmic music and cornrow hairstyles may
be the only traditional African fractal knowledge that continued in America.   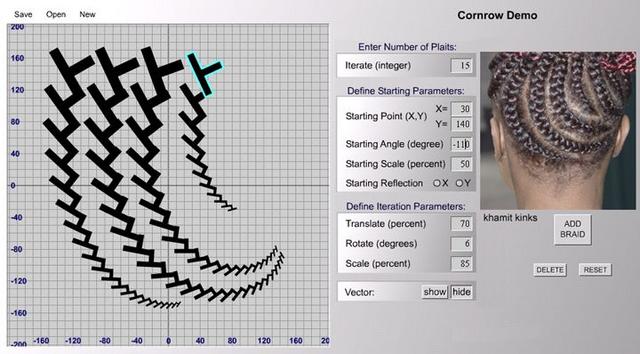 Cornrows show the fractal qualities of self-similarity, scaling,
and recursion (the output
of one braid is the input for the next, iteration). Cornrows - Wikipedia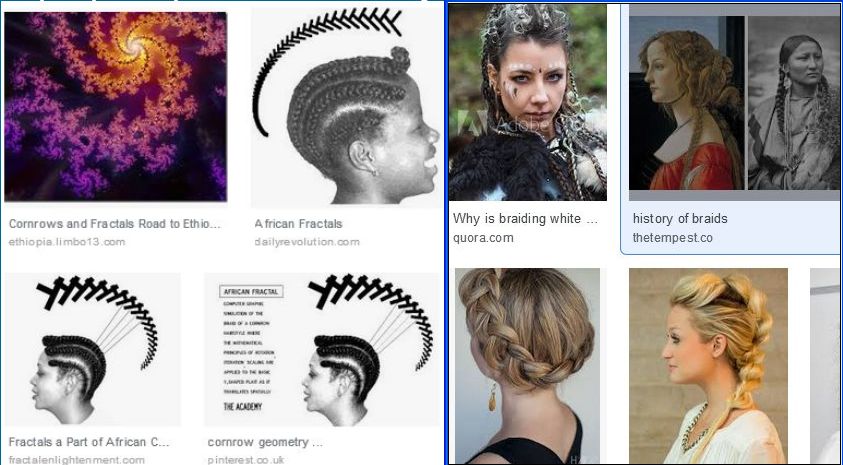 In the European, Asian, and Native American braided
hair styles (above on right) there is a different
pattern of the hair near the scalp as there is on the braids. In the European, Asian, and Native American braided
hair styles (above on right) there is a different
pattern of the hair near the scalp as there is on the braids.
In the African cornrows (above on left) there is the same pattern near the scalp as there is on the braids showing self-similarity, scaling, and iteration recursion.
The same difference in pattern is seen with the non fractal
pattern of traditional Native American and European architecture and the fractal pattern of traditional sub-Saharan African architecture.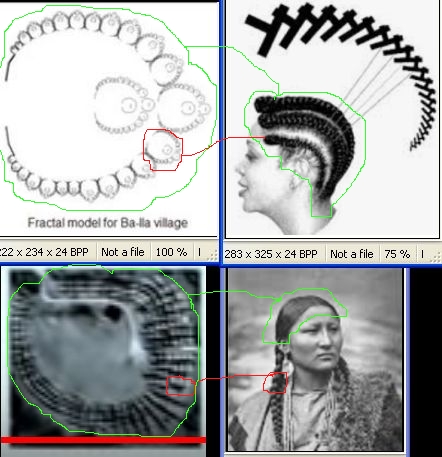 Above top pictures and red and green
projection lines show the sub-Saharan African
traditional cornrow hairstyles are fractal at one scale (green) and fractal at another scale (red). The same braided pattern at two different scales, the same
as the traditional African Ba-lia village architectrue which is fractal as a whole and at different scales. Above top pictures and red and green
projection lines show the sub-Saharan African
traditional cornrow hairstyles are fractal at one scale (green) and fractal at another scale (red). The same braided pattern at two different scales, the same
as the traditional African Ba-lia village architectrue which is fractal as a whole and at different scales.
Above bottom
pictures show Native American traditional braided hair style
is not fractal, as one scale or part near the scalp (green)
is a different pattern than the other scale or part on
the braid (red). Two different patterns just like with traditional Native American architecture like the Anasazi
which is circular at one scale and rectangular at another scale, not the same pattern. Fractals = self-similarity, scaling,
and recursion (iteration).
--- The relationship of the All-person to
individual man or woman is a fractal.
Jehovih saith "I AM within man and man is within me" =
a fractal relationship
"I AM within all things centering them, and I AM without all things controlling them"
- Walter Russell. <-----Fractal geometry, <------"The Ocean Lives Within
The Drop"-- <-----Fractal geometry, <------"The Ocean Lives Within
The Drop"--Fractal geometry (mathematics) = sacred mathematics (geometry) of the I'hins and the Israelites: Not only does fractal geometry and fractal mathematics
describe much of the natural universe, but fractals
also describe the relationship of the Creator and spiritual
man, such as:
Self-similarity (exactly or approximately similar,
sameness)
Scaling (tiny section looks similar to whole and Vice versa)
Infinity (unlimited extent, boundless)
Recursion (repetitive process)
Fractional Dimension (such as 1.26 dimensions,
infinite length in finite boundary)
Above are the five
essential components of fractal geometry - pages 17 -18 of African Fractals by Ron Eglash.
Oahspe Book of
Inspiration Chapter I:
1. ...I am Light; I am Central, but Boundless, saith Jehovih.
The central part is a fractal of the whole part (both containing boundless infinity, self-similarity).
Oahspe Book of Cosmogony and Prophecy ch 2:
26.
one light, with a central focus. [The Father-Creator is One Boundless Light with a
central focus, his central focus is man. Man is the focal point of the Father God]
Man is the fractal of the Creator-God.
Oahspe Book of Inspiration Chapter I:
12. As out of
corpor I made thy corporeal body, so, out of My Light, which
is My Very
Self, I built thee up in spirit, with consciousness that thou art.
"out of My Light, which is My
Very Self" = self-similarity = fractal.
Definition of very in US English:
adjective 1 Actual;
precise (used to emphasize the exact identity of a particular person or thing). 'those
were his very words'
"exact identity of a particular person" = SELF-SIMILARITY (fractal).
◄ John 14:11 ► of the Bible:
"I am in the Father and the
Father is in me" = fractal relationship.
The fractal (mathematical) universe:
Oahspe Book of Sue, Son of Jehovih:
Chapter V
16. God: I see nothing in all the universe but Thee! All selfs are but fractions of Thyself, O E-o-ih!
1/1000 = fraction = 1/1000
of Infinity = Infinity = a self-similarity fractal.
Google frac·tal: MATHEMATICS 1. a curve or geometric
figure, each part of which has the same statistical character as the whole.
Word Origin & History: fractal, 1975, from Fr., from
L. fractus "broken," pp. of frangere "to break" (see fraction).
Coined by Fr. mathematician Benoit Mandelbrot in "Les Objets Fractals."
- Relationship of fractals to phi (golden ratio):
2: The Golden Ratio as a Continued Fraction A
unique feature of the Golden Ratio is that it can be written as an Equation which calls itself:
Equation 1:
Phi = 1 + 1 / Phi This Process is called Iteration. Mathematical Iteration can also be used to generate a Fractal. at every scale. It is
also known as an expanding symmetry or evolving symmetry.
C'vorkum light-years numbers (when rounded to nearest whole number) show a fractal pattern of expanding symmetry.
Example 2727 (one whole C'vorkum) is a symmetrical expansion
of 909 (1/3 C'vorkum) 9 x 3 (expanded) = 27.
Both 2727 and 909 are symmetrical numbers (same numbers to
the left and right of center, 9-9 or 27-27).
--- In
this illustration below, every spiral is the same phi spiral repeated at different scales: ----------------------------------------------
The binary number system is an alternative to the decimal (10-base) number system
that we use
every day. Binary numbers are important because
using them instead of the decimal system
simplifies the design of computers and related technologies. -
Below: Binary code.  Above: Binary punched card.  Above is Internet Protocol address binary bits. -
"In Africa,
on the other hand base-2 calculation was ubiquitous, even multiplication and division.
...The implications of this trajectory--from sub-Saharan Africa
to North Africa to Europe are
quite significant for the history of mathematics. - Page 99 of African Fractals.
- Zaslavsky (1973) shows archaeological evidence suggesting that ancient Egypt's use of base-2 calculations derived from the use of
base-2 in Sub-Saharan Africa. - Page 89 of African Fractals.
- Eglash
explained that diviners use base-two arithmetic, just like the ones and zeros in digital
circuits, and bring each output of the arithmetic procedure back in as the next input. -
...the binary code appears
to have a distinct African origin (Eglash 1997a)
The modern binary code, essential to every digital circuit from alarm clocks to super-computers,
was
first introduced by Leibnitz around 1670. Leibniz had been inspired by the binary-based
"logic machine" of
Raymond Lull, which was in turn inspired by the alchemists’ divination
practice of geomancy (Skinner 1980).
But geomancy is clearly not of European origin. It
was first introduced there by Hugo of Santalla in twelfth century Spain, and Islamic scholars had
been using it in
North Africa since at least the 9th century, where it was first documented in
written records by the Jewish writer
Aran ben Joseph. The nearly identical system of divination
in West Africa associated with Fa and Ifa was first noted by Trautmann (1939), but he assumed
that
geomancy originated in Arabic society, where it is known as ilm al-raml ("the science of sand").
The mathematical basis of geomancy is, however, strikingly out of place in non-African
systems.
Unlike Europe, India, and Arabic cultures, base 2 calculation is ubiquitous in Africa, even
for
multiplication and division. Doubling is a frequent theme in many other African knowledge systems,
particularly
divination. The African origin of geomancy -- and thus, via
Lull and Leibnitz, the
binary code -- is well supported.
http://web.archive.org/web/20150430040344/http://homepages.rpi.edu/~eglash/eglash.dir/ethnic.dir/r4cyb.dir/r4cybh.htm Oahspe The Lord's Fifth Book:
Chapter VI:
29....and the seer sat therein, with a table before him, on which table sand was sprinkled. And the Lord wrote in the sand, with his finger, the laws of heaven and earth. -
Below: first three steps in Bamana sand
divination.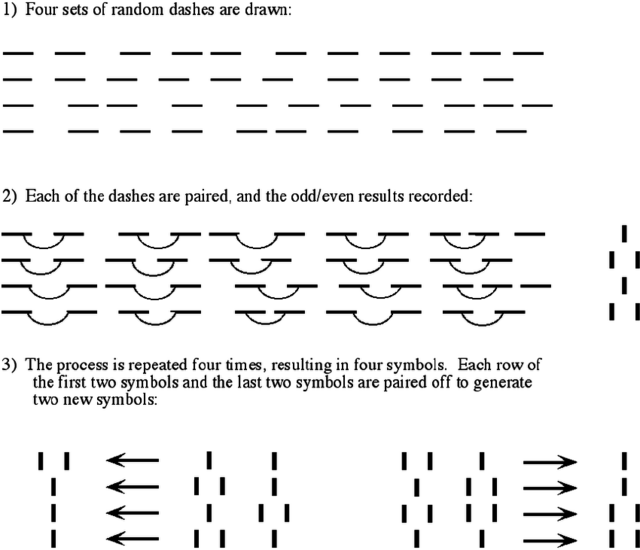 Below: 4th and 5th steps in Bamana sand divination.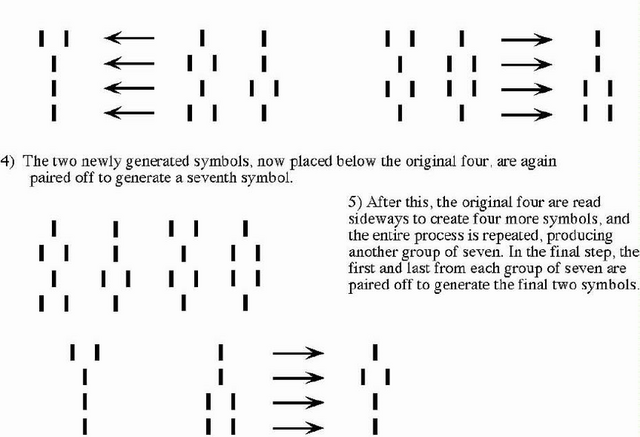 "I
did receive permission from my teacher to make the Bamana algorithm public. The TED format
only gives
you 17 minutes, and in that time I had to explain what fractal geometry is, how to
simulate fractals in African material
design, and what the connection is between the fractal
design and the indigenous knowledge. So I had to cut a lot of
details. I should also mention
that the divination priests told me that I was just reading a sentence or two from
whole
libraries of knowledge; the algorithm itself is
just one drop in their recursively infinite
bucket." - Ron Eglash, November, 2017
https://www.youtube.com/watch?v=7n36qV4Lk94 - ...the Bamana use recursion to generate a binary code in their divination,... - Page 124 of African Fractals by Ron Eglash. 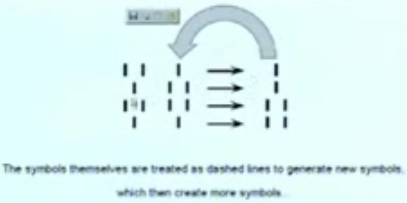 Above recursion
= the output of A+B = C (the input for the next iteration).  Above: from page 98 of African Fractals by Ron Eglash. Above: from page 98 of African Fractals by Ron Eglash.
Over 12,000 years ago,
Africans developed Ifa Oracle divination based on the square of 16 = 16 x 16 = 256 = 2⁸ corresponding
to the vertices of an 8-dimensional hypercube and to the binary 2-choice Clifford algebra
C1(8) and so to related ones such as C1(8) x C1(8) = C1(16). Since the number of sub-hypercubes in an 8-dimensional
hypercube is 6,561 = 81 x 81 = 3⁸, the Ifa Oracle has N = Earth Divination, Earth Magic: A Practical Guide to Geomancy ... A Comparative Study of Ifa Divination and Computer Science"The Yoruba gods of western Nigeria once existed as humans and had their way of communicating. Prior to
their disappearance, they left with the
people a means to communicate with them in the outer realm"
OAHSPE: Book of Saphah - M'HAK (Dark, or Degree of Golden Chamber.):
42. W.: Who are ethereans?
43. I.: Spirits who
have risen above the bondage of the earth and its atmosphere;
spirits who can come only to such mortals
as have attained beyond earthly desires.
24. W.: Who are the angels of heaven?
25. I.: People who once lived on earth or other corporeal worlds.
[1] An ‘orisha’ is a spirit or deity that reflects one of the
manifestations of the Creator (Olodumare) in the the Yoruba say: “Since Olorun is everywhere,
it is foolish to try to confine him/her in a temple”.
The Great Spirit has attendant spirits, children, agents or messengers
who ran errands and
who reflect aspects of the nature of the Great Spirit. The Yoruba call such beings Orishas,
and clearly
distinguish between them and Olorun. For the Yoruba, these Orishas
are many,
numbering 400 + 1 all the way up to 1600 + 1
[sacred numbers 400 and 1600, Dan and
etherean arc cycles each ruled by a different
Orishas or child of the Great Spirit], leaving
room
for humans to discover the multifarious dimensions or manifestations of the power
of Olorun. These Orishas
include: Orisha-nla (the Yoruba arch-divinity [arch or arc Angels],
and Olodumare’s deputy, who assisted in the creation of both the earth and human beings);
http://www.africanbelief.com/ Among
the K'iche' people of Guatemala, there is a myth that a flint
fell from the sky and broke into 1600 pieces, each of
which became a god. Thunderstone (folklore) - Wikipedia from the sky 1600 pieces = 1600 arc cycles,
each of which became a god = during each arc cycle the planet is ruled by a Etherean God such as Thor.
The oval flint stone = C’vorkum circuit or orbit.
https://www.etsy.com/market/thunder_stones This was an ancient Mayan belief that was a
remnant of the cosmic astronomical knowledge of the I’hins who landed in Guatemala (Guatama) after the sinking of the
Continent of Pan in the Pacific ocean. This 1600 number
of flint pieces is related to the 1600 number of Orishas of the Yoruba of Africa. One of the the Orishas of Yoruba is named Shango. Shango and the Norse God Thor and the Thor God(s) of Oahspe
resemble each other in several ways. The Marvel superhero known as Thor shares many of Shango's characteristics. Thor of Norse (Germanic) mythology
resembles Shango in just about every way except complexion! The above left image is the cover of a Marvel comic book. Illustrator Jack Kirby first
sketched Thor in 1962.May 17, 2019 shango: from sankofa to stan lee - write pon di riddim In the images above you have the Orisha Shango wielding a double ax similar to the MCU Stormbreaker
weilded by Thor. Alexander James Irons, read a lot of books Updated Mar 2, 2019 Originally Answered: Why Snorri identifies Memnon, King of Ethiopia who fought in the Trojan War, as the
father of Thor, in the Prose Edda? Isn't it Odin popularly considered Thor's father? A
king of Troj is named Múnón or Mennón. He owned the daughter of the main king Príamí. Her
name was Tróan. She had a son. His name was Trór, which we call Þór [Thor]. This passage is slightly
different in different manuscripts (the Uppsala Edda reads "There was a king named Menon.") but in the main is the
same. Interpreting this as Memnon, the Ethiopic king of the Posthomerica is pretty far-fetched. It's an obscure character.
I'd say it's fairly obvious from context this is a corrupted version of Agamemnon, who had Cassandra, daughter of Priam as
a concubine. A not-insignificant detail is that the verb owned ("átti") is used. So the names are just a
bit bungled; which Snorri does in lots of places in his prologue. (e.g. Saturn, not Zeus turns into a cow and abducts an unnamed
princess [Europa in the original] to Crete, and fathers Jupiter). - Edmund Davies · 1y No it’s not obvious that Mennon is a corrupted version of Agamemnon. They
are two different words, your speculating. He’s not obscure the Greeks knew who Mennon was. Just because Snorri decided
to make Saturn abduct Europa instead of Zeus doesn’t mean anything. I’m sure Snorri knows the difference between
Zeus and Saturn as well, it just simply means for whatever reason he decided to write his version of the story that way. - A Consumer · Jan 7 He wrote the truth but you can't handle it so you want to change it so it can bear
your prejudices. Oahspe Book of Sapah OSIRIS. 58. From Kosmon [1848], the present time, to Thor
(the first) - 15,400 years before Kosmon. Was the Etherean God Thor of the I'huan race? Was Thor a copper-colored Angel like Moses was
according to Oahspe? Thor's predecessor the Etherean God Apollo was born on the Continent of Pan before the submersion more
than 24,000 years ago and before the Ghan or Caucasian race apperared. On the Continent of Pan their was only the Asu, Druks,
Yaks, I'hins, and I'huans. Asu, Druks, and Yaks were born not capable of becoming an Etherean (everlasting life). Some of
the I'hins were black, brown and copper-colored as well as white and yellow before they sailed to Ham (Africa) or elsewhere,
so there was a moderate possibility that Apollo was a copper colored I'huan or a dark skinned I'hin as well as a white and
blond I'hin. Oahspe Book of Apollo, Son of Jehovih Chapter
II:1. I, Apollo, earth-born, of the continent Pan, submerged
by Aph, the Orian Chief, by Jehovih's command, ... Oahspe Book of Judgement: Chapter XXXIX:11. My angels shall appear before them, and
walk with them, talking to them, and teaching them of my kingdoms.12. And angels
of the I'hin race will come to them; and of the I'huans,
and of all other peoples whereof mention is made in this OAHSPE. - On Study of Oahspe
Misc. 3, Sacred mathematics, geometry, music, harmonics, cosmology, cycles page: about 1/5
down:
Cymatics harmonic sound made visible show very similar
geometric fractal pattern to snow flakes and Certain complicated cymatic
forms can be viewed as fractals, as their patterns
are often very complex and contain layers of patterns within patterns. Dec 1, 2011. Below are Wakandan Border Guards Opening The Country's Barrier using water drums
(from Marvel Movie Nov, 2022).  Water Drums (above) and rhythmic sound waves (cymatics) is used to open Wakanda’s barrier shield in the MCU (Nov 2022). The provenance of Cymatics
can be traced back at least 1000 years to African tribes who used the taut skin of drums... At 3835 Hz (above) we see similar symbol to Oahspe symbol (lines and shapes emanating
from cross probably ends in a circle). https://www.youtube.com/watch?v=wvJAgrUBF4w 3835 Hz is 59 x the fundamental C2 musical frequency of 65 Hz.587 / 65 = 9.03 = E523 / 65 = 8.04 = O329 / 65 = 5.06 = IH59 x = 5 and 9 = IH and E.9+8+5 = 22 / 3 = 7.333 average of E-O-IH (Creator's name).Similar symbol of Oahspe = 59 x / 7.333 x = 8.04 x harmonic multiple of E-O-IH average (8 represents
Harmany and light). At 5201 Hz (above) we can see another similar symbol to the Oahspe symbol. 5201 Hz / 65 Hz (fundamental C2 musical
frequency) = 80.015 a harmonic multiple. (8 x 10 = 80). 8 represents harmony and
light. 80.0 / 7.3 = 10.9589 (less than 0.05 from 11). Oahspe Book of Saphah: Se'moin 34: I'su (Panic). Ie-Su,...The true cross within Eloih Oahspe Book of Saphah: Plate 62. SE'MOIN: 9. Eloih, synonymous with E-O-Ih, the Creator,
the person who moveth the wind. The All Soul. The All Self. The Second Self, more subtle than the wind. It is the circumference
of all; it extendeth from left to right, and from below upward. 
Oahspe Book of Apollo, Son of Jehovih: Chapter XI:
2. Cim'iad was a small woman, dark, and of deep love,
most jovial of Goddesses; and had long looked forward with joy to her pleasure of bringing so large a ship to deliver two thousand
million of Jehovih's Brides and Bridegrooms into etherean
worlds. BLACK EXTRATERRESTRIALS, GODS AND GODDESSS DRIVING PLANETARY SIZE SPACE
CRAFTS   -
Practical
fractals: recursion in construction techniques...Williams goes on to note that much
African metal work, unlike European investment casting, uses a "spiral
technique" to build
up structures...resulting in ..."helical coils formed from smaller helical
coils." - Page 112
of African Fractals by Ron Eglash.
Figure 8.2-h A single iteration of a three-dimensional version of the recursive triangle construction, created by Akan artists in Ghana. [Ghana Akan worshipped
the Great
Spirit like the Israelites]. 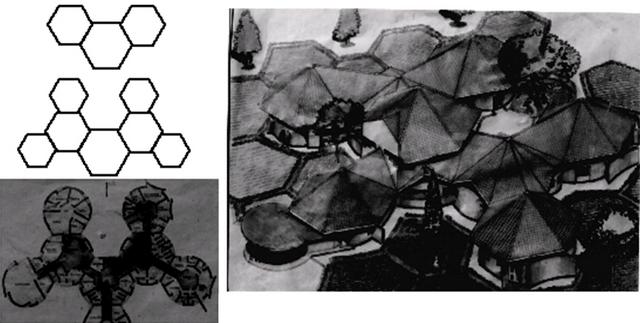 Above: Kitwe community clinic fractal design in Zambia, Africa by David
Huges and Alex Nyangula.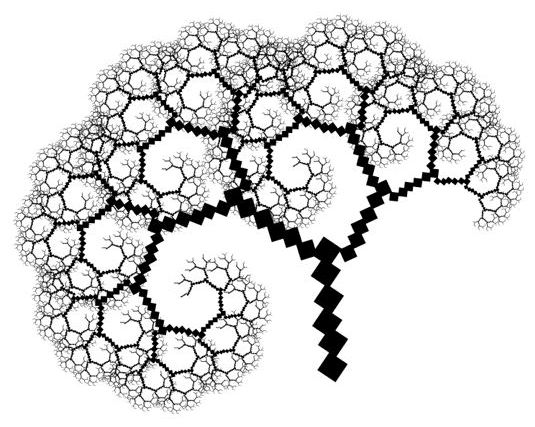 Above: Jola fractal settlement of Mlomp, Senegal - Page
163 of African Fractals by Ron Eglash. - Eglash described
an ivory hatpin from the Democratic Republic of the Congo that is decorated with carvings
of faces. The faces alternate direction and are arranged in rows that shrink progressively
toward the end of the pin. Eglash determined that the design
matches a fractal-like
sequence of squares where the length of the line that bisects one square determines the length of the side of the following square.
Above: Geometric analysis of
Mangbetu iterative squares structure of ivory sulpture
Pages 66-68 of African Fractals figure 5.5 ...the
construction algorithm can be continued
...applied to a wide variety of math teaching applications from simple
procedural construction
to trigonometry (Eglash 1998a).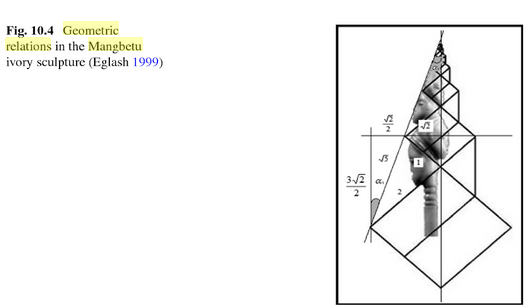 -
it·er·a·tion noun: iteration. the repetition of a process or utterance. repetition of a mathematical or computational
procedure applied to the result of a previous application,
typically as a means of obtaining successively closer approximations
to the solution of a problem. a new version of a piece of computer hardware or software.
-
Fractal geometry is a field
of maths born in the 1970’s and mainly developed by Benoit Mandelbrot.
The process by which shapes are made in fractal geometry is amazingly simple yet completely
different to classical
geometry. While classical geometry uses formulas to define a shape,
fractal geometry uses iteration. It therefore breaks away from giants such as Pythagoras, Plato
and Euclid and heads in another direction. Classical geometry has enjoyed over 2000 years of
scrutinisation, Fractal
geometry has enjoyed only 40.
How to make a fractal shape
The rules
are as follows:
1. Split every straight line into 3 equal segments.
2. Replace the middle segment with
an equilateral triangle, and remove the side of the triangle
corresponding to the initial straight line.
- 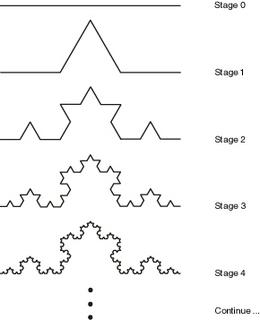 After this has iterated an infinite amount of times the fractal shape is defined. This may sound bewildering but it is still possible to analyse it mathematically and visually you can see what the shape starts to look like. The gif below (from Wikipedia) is a good illustration of what the curve looks like by zooming in on it: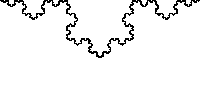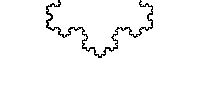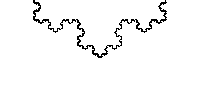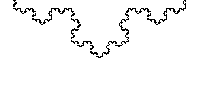 The von Koch curve [above looks exactly like a snowflake]
is a great example of a fractal: the rule you apply is simple, yet it results in such a complex shape. This kind of shape is impossible to define using conventional maths, yet so easy to define
using fractal geometry. Fractal trees: On the tree above, if you snapped a branch off it and stood it up, it would look like the
original
tree. If you took a twig from the branch and stood it up, it
would still look like the
original tree [self-similar]. Again, this is a property that occurs in nature,
but until fractal geometry there was not a good way to put it into maths.
-
Not
only do these shapes look like natural objects, but the process
of iteration sounds
intuitive when thinking about nature. When a tree
is growing, its trunk will create branches,
these branches create further branches, these branches create twigs. It’s
as if the function is
a genetic code telling the branch how to grow and repeat itself, eventually creating
shapes that
are ‘natural’. - Fractal
fibonacci numbers (sequence) and iterations:
-
A realistic map of the branching of a tree (or a variety of other plants too) is shown in the
figure below. In this case, the tree grows from the bottom
up, and the rule here is that a
branch grows one unit long in each iteration. When a branch is two units
long, it is strong
enough to support a node, which is where a new branch splits off. The branches alternate on the
left and the right, and very quicky a recognizable plant pattern emerges.
-
The rules that generate this fractal are really identical to the rules for the rabbit family
tree
above, since it takes two iterations for a branch in the rabbit family tree to bifurcate,
and it also takes a tree branch two iterations before it is strong enough to bifurcate.
The same
kind of self-similar pattern emerges,
because at any step you can look at a new rabbit pair, or
branch, as being the beginning of an entirely new sequence.
A little branch on a tree can be cut
off and planted and
will form a whole new tree. A grandchild rabbit can turn into the grandparent 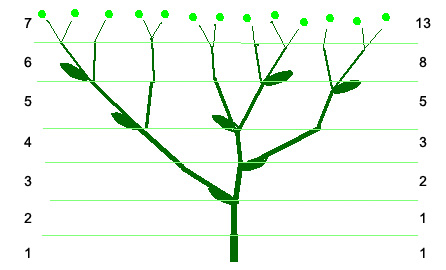 of many rabbits. Any
unit, at any iteration, is just a scaled version of any other unit in the system.
How many branches are there at the 6th generation? [ ] Above are shell and fern fractals, page 16 of African Fractals. -In theory,
one can argue that everything existent on this world is a fractal:
the branching of tracheal tubes,
the leaves in trees,
the veins in a hand,
water swirling and twisting out
of a tap,
a puffy cumulus cloud,
tiny oxygene molecule, or the DNA molecule,
the stock market
Fractals
will maybe revolutionize the way that the universe is seen.
A dissident
group of scientists claims that the structure
of the universe is fractal at all scales.
If this new theory is proved to be correct, even the big bang
models should be adapted.
The real world is well described by fractal geometry.Oahspe Book of Sue, Son of Jehovih: Chapter V
16. God: I see
nothing in all the universe but Thee! All selfs are but fractions -- fractals can occur over
time as well as space—one example is how hearts beat across at Harvard Medical School. Using graphs of heart rate time series
(like the 30-minute time series show
below), he quantified the "fractal-ness" of heartbeats across different scales. -
It may seem like sudden spikes and falls in the stock market are anomalous
flukes, but mathematician who is often called "the father of fractals." Based
on his belief that market fluctuations follow fractal geometry, he has created
fractal-based financial models that better account for extreme events than traditional
portfolio theory, which is based on a normal bell curve. Furthermore, these models
can be applied to any timescale, from years to hours.
-
Climate cycles and the rules of prophecy
in Oahspe are fractal in nature. 3.7 year cycle is a
1/3 fractal of the 11.1
year cycle. The 11.1 cycle is a 1/3 fractal of the 33.3 year cycle. The 33.3 year cycle is a 1/3 fractal of the 99.9 year cycle. The 1000 year cycle is a 1/3 fractal of the 3000 year cycle. The
11.1 year cycle divided into three 3.7 years is self-similar to the 33.3 year cycle divided into three 11.1 years, etc...
See "Cycles, Predictions, Earth events, A'ji" page of this website. - Using the golden ratio gets you the same proportion no matter what scale or how big or small you go…it is infinite in keeping the same proportion throughout whatever scale. Think in terms of the geometry and the Golden
Ratio Spiral. Each revolution retains the same proportion and is
therefore self similar, i.e. fractal. -
Fibonacci's Fractals (they are actually African in artistic & mathematic origin).
Indeed, these are not "Fibonacci's" fractals any
more than Georg Cantor's "Cantor set" was "Cantor's" i.e. European in origin. In both cases the
earliest documented human creative reproduction of nature's -
Badawy (1965) noted what appears to be use of the Fibonacci series in the layout of the temples of ancient Egypt. Using a slightly different
approach, I [professor Ron Eglash] found a visually distinct example of this [Fibonacci] series in the successive chambers of the temple of Karnak, as shown in
the figure 7.22. Figure 7.2b shows how these numbers can be generated using a recursive
loop. This formal scaling plan may have been derived from the nonnumeric versions
of scaling architecture we see throughout Africa. - Page 87-89 of African Fractals. Nonnumeric = geometric structure rather than numeric system. - There is no evidence that ancient greek mathematicians knew of the Fibonacci Series. There was use of the Fibonacci
series in Minoan design, but preziose (1968) cities
evidence indicating that it could have been brought from Egypt by Minoan architectural workers employed at Kahun." - Page 89 of African Fractals. Does the Parthenon really follow
the golden ratio? https://history.howstuffworks.com/history-vs-myth/parthenon-golden-ratio.htm -
...Known as recursive. The Fibonacci sequence was the first such recursive sequence known in Europe. - Page 97 of THE GOLDEN RATIO The Story of Phi by Mario Livio (Ph.D astrophysics).
- In the 1202 AD, Leonardo Fibonacci wrote in his book
“Liber Abaci” of a simple numerical sequence that is the foundation for an incredible mathematical
relationship behind phi. - "but
when it comes to the use of the Fibonacci series in the contemporary
history of mathematics
(cf. B rooke 1964), there is actually no evidence of a direct contribution from Fibonacci himself. By all accounts, German
astronomer Johanes
Kepler rediscovered the series independently in 1611, and it was only in the mid-1800s, with the formal publication of Liber Abaci, that french mathematician Edouard lucas found the Pisan historical predessor and named it accordingly. This fact has received little attention, and most texts present
Fibonacci's discovery as if it were in a direct intellectual line of descent rather than an honary title given to a well deserving but disconnected antecedent." - Page 206 of African
Fractals. - The golden ratio, a mathematical relation that often arises in fractals and other scaling geometries, ...structures derived from the golden ratio that organize typographic compositions and even structure living spaces also has presence in
traditional African architecture, and that this presence extends further back than sites and artifacts
in Greece...Eglash (1999). The first is the chief’s palace in Logone-Birni, Cameroon. This historical architectural site has a golden ratio scaling pattern embedded in its spatial design. The second is a similar scaling pattern in the Temple of Karnak from ancient Egypt. As Eglash notes, there is no evidence that ancient Greek mathematicians knew of the Fibonacci series (89). However Badaway
(1965) found a use of the Fibonacci series (1, 1, 2, 3, 5, 8, 13…) in the layout of temples in Ancient Egypt. Greek mathematician Euclid did describe dividing a line such that it created a golden ratio, but never discussed constructing a two-dimensional figure with that ratio.
The most famous representative of Greek architecture, Vitruvius, worked exclusively with proportions
that can be expressed in whole numbers, rather than irrational proportions that the golden ratio
would require.
This was in keeping with the ancient Greek distaste for irrational numbers and the infinite series,
which clashed with Platonic notions of mathematics as static perfection
existing in an eternal, unchanging ‘realm of the Forms.’ African designs, on the other hand, deliberately make use of such iterative sequences, since they fit well with the African cultural emphasis on fecundity,
fertility and cyclic aspects
of life. One can hear
this dynamicism in African polyrhythmic music, and see
it in iterative architectural designs
such as Karnak and Logone-Birni. The Temple
of Karnak from ancient Egypt shows successive chambers with lengths determined by iterations
of the Fibonacci Series. The altar in the temple of Karnak depicted in Figure 3 creates the initial value for the
generation of its form, just as we see for altars in other cases of self-generating architectural forms in Sub-Saharan Africa. Since archaeological evidence shows that Egyptian civilization
was founded when groups traveled down the Nilotic valley,[if the hebrews were originally nilotic (which they probably were),
haplo L2a (or possibly L2a1) would likely be their founding maternal haplogroup. it is no surprise that these traditions of recursive form were continued in Egypt. In the original sub-Saharan architectures the structures are not largely determined by quantitative formula; the Egyptian version thus provides
a more formal version of the sub-Saharan recursive tradition. It is not unreasonable to speculate
that Fibonacci brought the sequence from North Africa where it was used in the weights of a scale balance as well as architecturally. As shown in Figure 4 [above], we can postulate then that the golden ratio originated in Sub-Saharan Africa, migrated north possibly to Egypt, and then traveled to Italy and onward around the rest of the world. The two
historical African sites discussed in this paper are significant because of the well-known mathematical concept embedded in both of
their spatial designs—a phenomenon that has relevance to the history of communication design and African-American
design identity. Length of blocks of Logone-Birni Cameroon palace spiral path: 44 / 3.384= 13.0 for largest 28 / 3.384= 8.2 for middle 18 / 3.384= 5.3 for smallest Fibonacci sequence = ...5,
8, 13, ...  (approximate 3x and 1/3 scaling) in design. - Susantha Goonatilake writes that the development of the Fibonacci sequence "is Parmanand Singh cites Pingala's cryptic formula misrau cha ("the two are mixed")
and cites scholars who interpret it in context
as saying that the cases for m beats (Fm+1)
is obtained by adding a [S] to Fm
cases and [L] to the Fm−1 cases. He dates Pingala before 450 BC.[15] However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):
Variations of two earlier
meters [is the variation]... For example, for [a meter of length] four, variations of meters of two [and] three being mixed, five happens. [works
out examples 8, 13, 21]... In this way, the process should be followed in all
mātrā-vṛttas [prosodic combinations].[16]
Outside India, the Fibonacci sequence first appears in the book Liber Abaci - The Karnak Temple Complex, commonly known as Karnak ([1], from Arabic Ka-Ranak meaning "fortified village"), comprises a vast mix of decayed temples, chapels, pylons, and other buildings in Egypt. Construction at the complex
began during the reign of Senusret I [from 1971 BC to 1926 BC] century BC and
the 11th century BC]. "Reevaluating all of the existing material in this light, I have to conclude
that it is very unlikely that the Babylonians discovered the Golden Ratio."
- Page 47 of THE GOLDEN RATIO The Story of Phi, The World's Most Astonishing Number by Mario Livio. The
Fibonacci sequence, logarithmic spiral and Golden Ratio scaling
(a fractal scaling ratio) go hand in hand. 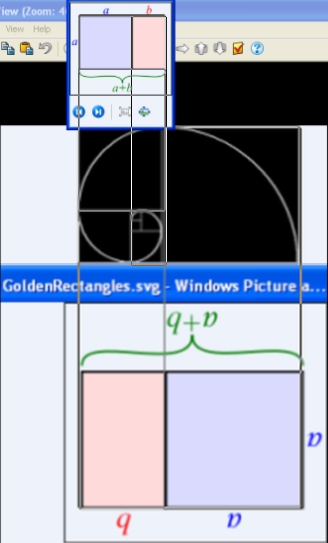 Above: Golden Ratio Fibonacci spiral and Oahspe cyclic coil of the Great
Serpent of the solar system. Both showing decreasing in size twists. Above: Fractals of neurons in brain (see dark matter network below) and passages in lungs. Above: Etherean worlds and roadways have fractal architecture. Oahspe God's Book of Ben Plate 44 -SNOW FLAKES [Snow flakes are symbols of Etherean worlds]. Look at the snowflakes as though they
were microscopic
patterns of the worlds in high heaven. Above: many traditional
sub-Saharan African villages have fractal architecture.  Above: On the left is Mokoulek fractal village of Cameroon, Africa. On the right is model
of Our "fractal"
universe (showing self-similar spirals and circles at different scales). A traditional branching fractal settlement in Senegal, page 35 of African Fractals. - ...a wide variety of African settlement architectures can be characterized as fractals. Their physical construction makes use of scaling and iteration,
and their self-similarity is clearly evident from comparison to fractal graphic simulations...fractals
in African architecture...is linked to conscious knowledge systems that suggest some of the basic concepts of fractal geometry,...we will find more explicit expressions of this indigenous
mathematics in astonishing variety and form. - page 38 of African Fractals. - 1.1
Definition of Fractal The formal mathematical definition of fractal
is defined by Benoit Mandelbrot. ... Generally, we can define
a fractal as a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole. - Below logarithmic spirals and fractals: Smaller pyramid within smaller spiral in center is a fractal of larger pyramid within larger spiral.
Below: Logarithmic scaling and Great Pyramid of Egypt:
Figure Three shows a graph of the mean orientation among structures on a log scale. This
produces a linear
decline according to pyramid number. The measured values hold amazingly well
to a mathematical equation expressing the
decay, with small variance from the regression line.
 The mathematical expression for this line is: The mathematical expression for this line is:
Y = A (intercept at 0 pyramid number) - B (slope) (pyramid number).
or
Y = A - B X P where P denotes the pyramid
number.
Note that we are now dealing with logarithmic numbers
on the vertical scale, not linear numbers.
The orientations are expressed in the natural logarithm of the original number, while the pyramid
numbers are
expressed on an ordinary linear scale.
For those who may not be acquainted with logarithms, two forms are commonly used
in mathematics
and the physical sciences. The first is called "common logs" based on multiples
of 10. 100 = 1,
101 = 10, 102 = 100, and so on. The second is called "natural logs" based on an important
physical constant we symbolize by the letter e = 2.71828. e0 = 1, e1= 2.71828, e2 = 7.389, and
so on. e most often
expresses the rate of natural decay processes.
In following discussion I shall use the symbolism of log to denote common
logs, and ln to denote
natural logs, following common practice in modern scientific and technical fields.
We might
argue that the data from the pyramids are not natural; they do not come from natural
processes. They were devised by
human intelligence and control. However, the data plots show
that the designer prearranged his structures to express
a curve similar to natural decay. He
probably did so because he knew that anyone competent enough to detect the form of the curves
would be familiar with natural processes.
He also had to be familiar with natural decay
processes, and how they are expressed mathematically, otherwise he could
not imitate them.
After I calculated the intercept and the
slope of the orientations from the data on the basis
of a natural decay curve I bumped into another amazing
value. The intercept was 10 Pi and the
slope was very
nearly 1/Pi or possibly Pi/10. I show both the regression line calculated from
the data (solid) and the
two theoretical lines (dashed) on Figure Three.
We saw in the Great Pyramid Pi chamber that the designer used (Pi X ln
10) for one of his
dimensions to show his knowledge of
higher mathematics. Here he displays it with the intercept
values and the slope of the logarithmic decay.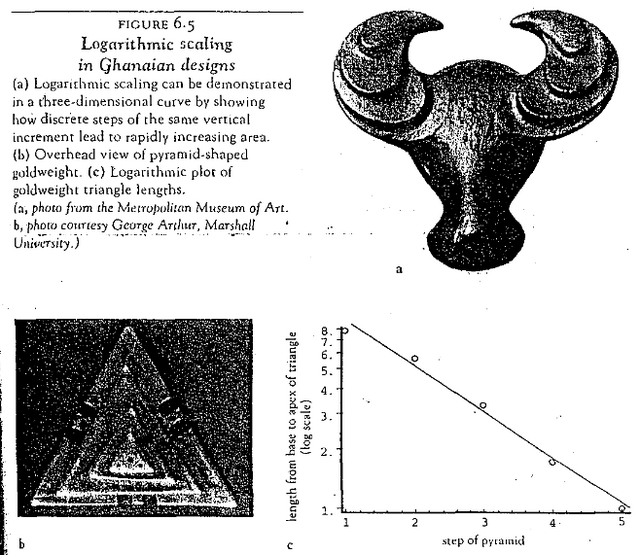 Above: logarithmic scaling in Ghanaian design - African Fractals by Ron Eglash page 79. Above: logarithmic scaling in Ghanaian design - African Fractals by Ron Eglash page 79.- How a Galaxy is a Fibonacci Sequence: Physics & MathAbove I have mapped
the slope angle of the Great Pyramid of Egypt using a basic coordinate system similar to the way
longitude (vertical) and latitude (horizontal) coordinates are demarcated on a map. Left side vertical
coordinates / right side horizontal coordinates. Coordinates of
Great Pyramid logarithmic fractal slope:
2/3, 3/5, 5/8, 8/13, 13/21 ... = left/right, vertical/
horizontal coordinates. Horizontal / vertical-slope = (13/8) 1.625.
0,1,1,2,3,5,8,13,21,34, ..... = Fibonacci Golden ratio (Phi) sequence.
Notice the vertical coordinates
/ horizontal coordinates of the Great pyramid
Logarithmic slope are Fibonacci (Phi) numbers. The coordinate numbers
approximate the Golden Ratio (Phi), just as a spiral galaxy is a close approximation of a Fibonacci golden ratio logarithmic spiral. 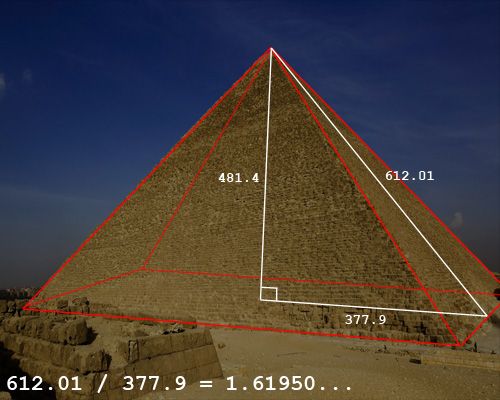 Great Pyramid Fibonacci Sequence Slope / horizontal = 1.61950 Great Pyramid Fibonacci Sequence Slope / horizontal = 1.61950 The+golden+Ratio+in+History-Great-Pyramid https://slideplayer.com/slide/13070967/79/images/11/The%20golden%20Ratio%20in%20History.jpg https://projectlibertas.files.wordpress.com/2013/01/fibonacci-design-pyramid2.jpg golden ratio.[1] That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. The logarithmic
spiral is also known as the growth spiral, equiangular spiral, and spira
 https://web.archive.org/web/20170315143333/https://geekgirldecodes.com/2017/03/14/recursive-functions/ https://web.archive.org/web/20170315143333/https://geekgirldecodes.com/2017/03/14/recursive-functions/- "Generating the Fibonacci series requires a feedback
loop or, as mathematicians call it, iteration.In iteration, there is only one transformation process, but each time the process creates an output, it uses the result as the
input for the next iteration, as we've seen in generating
fractals." - Page 110 of African
Fractals. -------- Fibonacci Sequence and 5 fractal characteristics: Scaling,
self-similarity, recursion, infinity, fractional dimension. Scaling (small to large scale): 2/3 = 0.667 3/5 = 0.6 <---Self-similarity (same
ratio aprox. 0.6) 5/8 = 0.625 8/13 = 0.615 13/21 = 0.619 21/34 = 0.618 (golden ratio) Recursion (feedback loop, iteration, output becomes
input): 2+3 = 5 <---A+B = C 3+5 = 8 <---take C and add
it to B 5+8 = 13 <---each number is the sum of 2 previous numbers. 8+13 = 21 13+21 = 34 21+34 = 55 Infinity: 1,2,3,5,8,13,21,34,55,89,144,...----->
infinity. 0.6180339887498948482...<--Golden Ratio--> infinity. 0.618 = fractional dimension.  ------------------------------------------------------------------------------------- Fractal mathematics is a part of the religion and SPIRITUALALITY
of sub-Saharan Africans
(original Israelites) considered sacred
by the priests they did not want to voluntarily teach it to professor Ron Eglash
until he showed them the Cantor set. 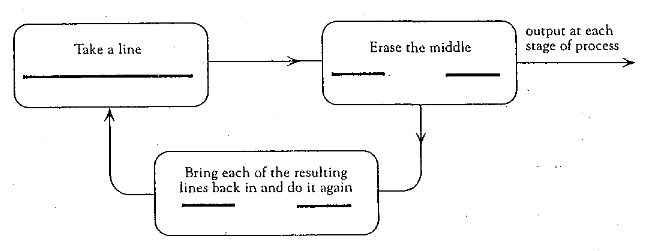 Above: Cantor set is created by recursion (iteration). -
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. The Cantor set is the prototype of a fractal. It is self-similar, because it is equal to two copies of itself, if each copy is shrunk
by a factor of 3 and translated. More precisely, there are two functions, the left and
right self-similarity transformations,  and and  , which leave , which leave the Cantor set invariant up to homeomorphism:  Repeated iteration of Repeated iteration of
 and and  can be visualized as an infinite binary tree. Cantor set - Wikipedia can be visualized as an infinite binary tree. Cantor set - Wikipedia
 2) Brain regions involved with mystic experiences. ...are the amygdala and hippocampus. A mystic whose experiences appear from an unusually responsive right hippocampus is expected to report experiences dominated by right hippocampal (RH) phenomena. The RH role in spatial reasoning
and memory implicates it in experiences of 'infinity', the "infinite void", spaciousness, and the experience
that the space occupied by the sense of self is limitless ("one with the universe"). The RH role ...Its cognitive functions implicate it
in the experience of 'knowingness', and 'insight', in which understandings appear spontaneously. - Mysticism ....may also refer
to the attainment of insight in ultimate or hidden truths,
,,,
The science of fractals lies on
the edge of infinity. Recent mathematical developments like
fractal geometry represented the top of the ladder in most
western thinking, he said. "But
it's much more useful to think about the development of
mathematics as a kind of branching structure and
that what blossomed very late on European
branches might have bloomed much earlier on the limbs of others. 8. Oahspe description: Oahspe
First Book of God 8:7: Abram was of pure blood, an I'huan;Oahspe Book of the Arc of Bon 15:13 Moses grew and became a large man, being a pure I'huan, copper-colored.  Above are Sub-Saharan African interlace knot symbols.  Above Maori spiral design tattoo and Maori warriors from New Zealand. Above Maori spiral design tattoo and Maori warriors from New Zealand.in all regions of this vast territory,
Many sub-Saharan languages do not
have a word for rhythm, or even music. Rhythms represent the
very fabric of music in the world. Rhythms and counter rhythms in the common African tradition of call and response
complement and communicate with one another with different drum lines, other
musical instruments, bodies and voices contributing rhythmic elements. This
element of instrumental call and response is also evident in
the polyrhythmic Drums of Passion, which was a collection of traditional Nigerian music for percussion and chanting. The album stayed on the charts for two years and had a profound impact on jazz and American popular music.[citation
needed] Trained in the Yoruba sakara style of drumming, Olatunji would have a major impact on Western popular music. [citation needed] He went on to teach, collaborate
and record with numerous jazz and rock artists, including Airto Moreira, Carlos Santana and Mickey Hart of the Grateful Dead.
Olatunji reached his greatest popularity during the height of the Black Arts Movement of the 1960s and 1970s.
Among the most sophisticated polyrhythmic music in the world is south Indian classical Carnatic
music. A kind of rhythmic solfege called konnakol is used as
a tool to construct highly complex polyrhythms and to divide each beat -
"Keep in mind that, hands down, the most rhythmically complex music
known is commonly considered by musicologists to be West African. (The
next, IMO, is likely the ragas of India.) It seems that some appropriate mention of the cultural context of the phenomenon is in order here -- perhaps a mention of how European classical music is, and much of Western music (before African/African-American influence) was, heavily
linear and flat/unsyncopated."
- deeceevoice 12:21, 5 December 2005 (UTC)
"Since no one else saw fit to add anything about the true origins of
polyrhythmic musical expression in Western music, I did so. It's outrageous
to mention Zappa and white musicians and no mention of the source, Africa. Someone
might also want to mention the ragas of India, where the sounds of the tabla correspond to spoken The basic musical forms taught to beginning musicians are usually accompaniment
parts of polyrythmic ensemble pieces. Polyrhythm, quite simply, is an African Music 101 topic. In Western classical music, polyrhythm really is a fringe curiosity, and when it shows up, it
is treated as an advanced topic.
There's also the fact that citing 20th century classical composers as
an example is problematic on other grounds—20th century European art
has in many cases looked to African arts for inspiration ..."
- (talk) 19:59, 17 July 2008 (UTC), Spot-on. Co-signing.
My point(s) precisely! ;) deeceevoice (talk) 12:20, 3 August 2009 (UTC) - "A good example of this nonlinear scaling can be seen in the logarithmic spiral." - page 76 of African
Fractals. -   Even when recursion does
come up in the fractal geometry literature, the
treatment is Even when recursion does
come up in the fractal geometry literature, the
treatment is typically informal
or cursory. For example, Saupe (1988, 72) merely notes that "in some cases the procedure can be formulated as a recursion." ...On
the contrary,
but that ...is impossible without it [feedback loop]. - Page 214 of African Fractals by Ron Eglash.   Above magnification zooms of Mandelbrot set showing bifurcation (branching) fractals.  The logarithmic spiral depicts
growth and expansion in the universe, and the edges of the Mandelbrot set fractal depict growth and expansion in infinite space. Above (branching and logarithmic spiral) shows as
the spiral expands the number of branches in the tree increases. 
OAHSPE GOD'S BOOK OF BEN CHAPTER VII:
3.
I am the living mathematics; - How do cells duplicate (replicate) themselves, and why? In all complex multicellular
organisms (eukaryotes), cell duplication occurs by a process called "mitosis" or cell division.
Growth. We all started
out as a single cell; the fusion of a sperm from dad and an egg from mom. That original cell divided repeatedly until you grew
and differentiated into an organism composed of billions of cells. But this raises an interesting
problem. When one cell divides into two, both must have a copy of the genetic information.
Therefore, before cell division occurs, the genes must also make duplicates of themselves
so that all of the important genetic information ends up in each of the new cells. The first cell divides into two, and each of those two divide again, and this process
continues geometrically along the following progression: 1, 2, 4, 8, 16, 32, 64, 128, and so on
into the billions. That's growth.
- Computer code bits is in harmonic multiples and divisions of 8. The two (2) base system (bi-nary, base 2 calculation) is a harmonic division of 8. Multiply 1 x 2 x 2 x 2 x 2 = 4, 8, 16, 32 which are
harmonic parts (divisions) or multiplications of 8 which are 1, 2, 4, 8,
16, 32, 64, 128, 256, 512, etc...start off with 1 whole and multiply x 2, x 2, x 2, x 2, x 2, x 2, x 2, etc... you get all divisions or multiples of 8, like harmonic musical notes or computer bits.
Computer binary code 8 bit-system (each number below represents a iteration in the recursive branching fractal process):
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768.
http://stackoverflow.com/questions/8630344/understanding-binary-code
- " If you want to reveal the handiwork of God and see his design
and order in all things, fractals will reveal that design to you." - WHY DO FRACTALS
OCCUR BOTH IN MATH, WHICH IS ABSTRACT(not made up of atoms) AND
THE PHYSICAL WORLD, WHICH IS PHYSICAL(is made up of atoms)? The same designer (Jehovih). Mandelbrot image (left) and branching lightning (right).  Mandelbrot image (left) and snowflake (right).  Barnsley fern (left) and nature fern (right). One sort of fractal is known as the Iterated Function System, or IFS. This Barnsley fern (left) and nature fern (right). One sort of fractal is known as the Iterated Function System, or IFS. This fractal system was first explored by Michael Barnsley at the Georgia Institute of Technology in the 1980s. You start with shapes
plotted on a graph, and iterate
the shapes through a calculation process that transforms them into other shapes on the graph. Starting with four shapes, one of which is squashed into a line segment
(this becomes the fern's rachis or stalk), you apply the shapes to the calculation to generate more shapes, feed them back into the calculation process, etc. Eventually
a pattern Math generated fractal (left) and window frost (right).  Mathematical graph shape (left) and Romanesco broccoli (right).  Mandelbrot set logarithmic spiral (left) and spiral galaxy (right).  Above: African Ba-ila settlement fractal of Zambia early 1940s (left), fractal circles of the Mandelbrot set
(center), Mandelbrot
set main bulb fractal (right). The
Mandelbrot set ... This fractal was first defined and drawn in 1978 by Robert W. Brooks and Peter Matelski as
part of a  Above: fractal pattern of Songhai village in Mali (left and center). Others suggest the village is an conscious expression
of a fractal structure that became a cultural construct of many regions in Africa. Notice the similarity of the African Mali village layout to the Julia set fractals (right). - Arthur
C Clarke - Fractals - The Colors of Infinity.
From 7:50 to 8:21 of video:
the seeds to this discovery were in fact sown decades before the M set was first seen,
in Paris in 1917 a mathematician called Gaston Julia
published papers connected with so-called complex numbers,
the results of his endeavors eventually became known as Julia sets although Julia himself never saw a Julia set he could only guess at them [his guesses were way off]
and it wouldn't be until the advent of - The
Mandelbrot set (named after Benoit Mandelbrot)
is the most famous fractal of all, and the first one to be -
Ron Eglash was exposed to the fact that the knowledge and application of
fractals had been alive for millennia in Africa.
This concept of infinity had for long, before Cantor,
been part of the African divination system. In Africa, Eglash encountered some of the most complex fractal systems that exist in religious activities, such as the sequence of symbols used in sand divination, a method of fortune telling
found in Senegal. The concept of infinity had a metaphysical link with infinity.
The relevant point is that fractals existed in nature and before Mandelbrot there was Koch and Cantor. Fibonacci Numbers hidden in the Mandelbrot Set: - Mandelbrot
Set Fractal Zoom 10^227 [1080x1920]
"the Mandelbrot
main structure is repeated infinitely, but each structure has more pattern than the previous one".
"This is beyond amazing".
"I have a hard time believing this is real".
https://www.youtube.com/watch?v=PD2XgQOyCCk Eye of the Universe - Mandelbrot Fractal Zoom (e1091) (4k
60fps)
- Oahspe
Book of Lika, Son of Jehovih: Chapter VII:
1...in the
etherean sea, moving brilliants playing kaleidoscopic views, ever changing the boundless scene - The Mandelbrot fractals contain worlds without
end. Oahspe Book of Ouranothen CHAPTER 1: 8. First, then, His Living Presence I declare to you; that He is now, always was, and ever shall be present
in all places, worlds
without end. - Oahspe
Book of Discipline: Chapter XIV: 21. ...by Jehovih, Creator, Ruler and Dispenser,
worlds without end. Amen! - The Mandelbrot fractal is like Infinite
reflections in a mirror:  A computer can magnify (zoom-in) infinitely (or to 227 orders of magnitude) so you can
see more. A computer can magnify (zoom-in) infinitely (or to 227 orders of magnitude) so you can
see more. Infinite self-similarity, Infinite
complexity, Infinite scaling, Infinite repetitions, Infinite universe contained within a fractal. The Mandelbrot set
fractal is created by recursion and iterations of a mathematical formula Z = Z2 + C (x2
+ c).    - areas in
the fractal. The
Amazing Mandelbrot Set tutorial: - "Modern computers have given us the ability to peer deep into the complex plane
opening up a whole new world of mathematical wonder." "But computers can't give us the power to understand what we may discover a link between the Mandelbrot Set and the processes that guide the laws of nature."
- The end of The Amazing Mandelbrot Set tutorial video.  3:39 into video: "The easiest
way to simulate a world as realistic as possible is to use fractal formulas". 3:50 to 4:29 into video: "The first completely
computer generated movie seen in a feature film was the fractal animation of a planet in Star Trek 2
The Wrath of Khan. The Lucas film group responsible
for this was later acquired by Steve Jobs, from this he
created PIXAR thus revolutionizing Hollywood, they're animated movies look so realistic because the generated landscapes are based on the fractal principle of self-similarity, progress
has continued and today these elaborate and costly movie seens have evolved into real-time walkable game worlds like the landscapes of Minecraft". Holographic = realistic 3D simulation. Fractal formulas = mathematical
recursion, iteration, feedback. - Study reveals substantial evidence of holographic universe.
The idea is similar to that
of ordinary holograms where a three-dimensional
image is encoded in a two-dimensional surface, such as in the hologram on a credit card. However, this time, the entire universe is encoded!” Although not an example
with holographic properties, it could be thought of as rather
like watching a 3D film in a cinema. We see the pictures as having height, width and
crucially, depth – when in fact it all originates from a flat 2D screen. The difference,
in our 3D universe, is that we can touch objects and the ‘projection’ is ‘real’ from our perspective. https://www.southampton.ac.uk/news/2017/01/holographic-universe.page Living
in a MATRIX hologram – scientists say EVERYTHING we see could be an illusion
Jan
30, 2017 - EVERYTHING in the universe could be a "complex
hologram" meaningall that we see in 3D
is actually
an illusion. https://www.dailystar.co.uk/news/latest-news/583590/Universe-hologram-theory-science-expert-experts-world-mystery-solved-physics-hologram - Oahspe God's Book of Ben: Chapter II:
24. Nor is there aught in thy corporeal knowledge that thou canst prove otherwise, save it be thy presence;
and even
that that thou seest is not thy presence, but the symbol
and image of it, for thou thyself art but as a seed, a spark of the All Light, that thou canst not prove
to exist.
Chapter V
17. Uz said: All thou seest and hearest, O man, are but transient and delusive.
- Something incredible – and deeply perplexing – is currently taking place at the
intersection of mathematics,
religion, design technology and computer science; something that could fundamentally
alter the way we perceive
reality.
Over the past few years, several prominent mathematicians have claimed to have discovered a connection
between a mysterious mathematical
sequence and the very structure of our universe, speculating that it is possible
to express nature's immutable laws
in a complex geometric image.
the Mandelbrot set, may be a geometric depiction of an "eternally existing self-reproducing chaotic and
inflationary universe"
and can only now be rendered in full detail by using state
of the art computer technology.
Mandelbrot used fractal
geometry and funky color schemes to demonstrate
mathematically that infinity is real and
exists even in a world that appears finite to the naked eye.
This is where shit gets deep - evoking the concept of God
and the idea of eternity.
- Roger
Penrose. He is a mathematical Platonist, and believes that both the fractals worlds (such as the Mandelbrot
set) and the mathematical truths (such as Fermat’s last theorem) are discovered. In his view, the mathematical truths have an eternal, unchanging, objective existence in some kind of Platonic ideal world, independent of human observers. - fractal simulations for natural objects
are created with a "seed shape that undergoes recursive
replacement". - page 12 of African Fractals. A'su seed
shape undergoes recursive replacement
by adding angelic genes ( I'hin) into the mix. Like fractals the Kosmon race in Oahspe is created by additive recursive feedback loop iterations:  - 0.
A'su = no mixbreeding 1. start with seed shape A'su, breed A'su with
Ethereans (who died in fetal or infancy) = output I'hins. 2.
take the output I'hins and breed back to A'su = output Druk 3. take the output Druk and breed back to
I'hin = output I'huan 4. take the output I'huan and breed back to I'hin = output Ghan 5. take the output Ghan and breed back to I'huan = output Kosmon. - Number of iterations on the left (above). Takes 5 iterations of breeding to make the Kosmon race, the goal of Jehovih. 5 = balance (center of 0-10, 1-9). 5 is a Fibonacci number.  The
most balanced complete "perfect" man (race) was created
using fractal principles of recursion
and feedback loop according to Oahspe and the fossil record this is the same way Jehovih created the fractal universe of nature which is different from the Biblical story in Genesis. Like a fractal the races of man in Oahspe
are generated by a recursive feedback loop of 5 iterations from I'hin to Kosmon. Recursive
feedback loop formula for generating the present and future races of mankind: A'su
= A, I'hin = C, Druk = D, etc... A + B = C. (C is the output). C
+ A = D (C is the first input that was an output). D + C = E E + C = F F
+ E = G Generating the present and future races of mankind involves recursion, self-similarity, scaling, and infinity = Fractal. I'hin,
I'huan, Ghan, and Kosmon are self-similar to each other
with everlasting (infinity) life. The I'hin was half the size (scaling)
of the I'huan, Ghan, and Kosmon (1/2 and 2x). The races of man in Oahspe are generated by
recursion (the output at one stage becomes the input at the next stage). The output is a previous race, the
input is the creation of a new (or different) race. In the Bible, Man (Adam) is
created whole complete and "perfect" at the beginning with no
build up or use of recursion or mix-breeding, the same with Noah. In Oahspe Adam (A'su) was not whole or complete and neither was the I'hin. The way Oahspe says the races of man were created
agrees with the fractal processes of nature we
observe everyday, the way the Bible says the races of man was created does
not agree with the fractal processes of nature we observe everyday. What scientists call human evolution is just iterations of a recursive process of mix-breeding.  How the races of man in Oahspe is like a Fibonacci sequence (recursion): Each race is the sum of its two predecessors: A + B = C A
+ B = two predecessors or input, C = sum or output. The output becomes the input for the
next number. C + A = D and so on. According to Oahspe
even though the first manlike creation (A'su) was not the result of mix-breeding he
was the result
of recursion (sum of its predecessors). Oahspe
BOOK OF INSPIRATION. CHAPTER VI: 19. Nevertheless, I had given to man, and thus made him, out
of the dissolved elements of
every living thing that had preceded him. Ouput becomes the input (recursive process of generating a fractal): "out of the dissolved elements of every living thing
that had preceded him". Oahspe
Book of Inspiration Chapter I: 8. Thou wert nothing; though all things that constitute thee, were before. 9.
These I drove together, and quickened. Here
(above) Oahspe explains how Jehovih created man (recursion), not
from nothing, but from
that which was before, these parts Jehovih brought together (a creation). "When life gives you an ancient cave filled with dirt, look for DNA. That's what
paleontologists and those involved in the study of ancient humans will likely
be doing in the future following the revelation of a breakthrough technique that enables hominin DNA to be recovered directly
from sediments without the need for fossils."
Ancient human DNA found in dirt, not fossils -
New Atlas The study has been published in Science. Soil is composed of a matrix of minerals, organic matter, air, and water. http://organiclifestyles.tamu.edu/soilbasics/soilchemical.html 1
Corinthians 15:47 The first man was of the dust
of the earth, the second man from heaven. OAHSPE: First Book of the First Lords CHAPTER I. 4.
And the name of the first race was Asu (Adam), because
they were of the earth only; and the name of the second race was I'hin (Abel), because they were capable of being taught spiritual things. Can mere mathematics create an entire universe? The
Mandelbrot set fractal is created by recursion and iterations of a mathematical formula
Z = Z2 + C. Physical structure follows mathematical fractal laws. Physical form on the right follows mathematical recursive iterated
function (Z = Z2 + C) on the left.
Images on the left are self-similar to
the images on the right. Images below shows how the infinetely complex forms in nature could possibly form. 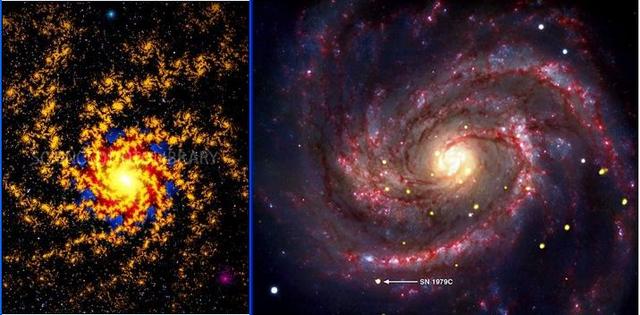 Abstract Mandelbrot
fractal image and spiral galaxy M-100 in
physical space.  Abstract Mandelbrot zoom
and Hubble Space Telescope image of quasar
and host galaxies. Abstract Mandelbrot zoom
and Hubble Space Telescope image of quasar
and host galaxies.  Abstract Mandelbrot Fractal
Zoom and M102 lenticular galaxy and planet
Saturn in physical space.  Abstract Mandelbrot fractal zoom and 8 petal flower in physical nature. Abstract Mandelbrot fractal zoom and 8 petal flower in physical nature. Abstract Mandelbrot fractal zoom and 4 petal white flower in physical nature.  Mandelbrot fractal zoom
and Planetary Nebula Ethos 1 (circle and cross)
and stars in space. Mandelbrot fractal zoom
and Planetary Nebula Ethos 1 (circle and cross)
and stars in space.
 Mathematical Mandelbrot fractal zoom
and Elephants with coiled trunk and walking in line
in physical nature. Mathematical Mandelbrot fractal zoom
and Elephants with coiled trunk and walking in line
in physical nature. Abstract Mandelbrot fractal
zoom and Autumn forest trees with no leaves in
nature. 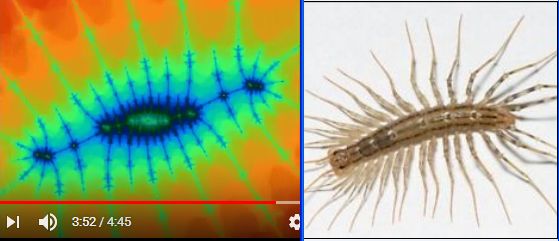 Abstract Madelbrot fractal zoom
and Centipede Chilopoda classification in nature. Abstract Madelbrot fractal zoom
and Centipede Chilopoda classification in nature. Abstract Mandelbrot set zoom
and Pterodactyl Fossil body in physical nature.  Abstract
Mandelbrot-Julia set hidden structure and White
tip shark in physical nature.  Abstract Mandelbrot-Julia
set fractal zoom and Sunflower Asteraceae plant
in physical nature.   Mandelbrot fractal zoom
and Luidia australiae seastar. Mandelbrot fractal zoom
and Luidia australiae seastar. Mandelbrot fractal zoom
and DNA double helix scanning electron microscope
image. Mandelbrot fractal zoom
and DNA double helix scanning electron microscope
image.- Although the Mandelbrot set images start out from one simple
equation (Z = Z2 + C) due to the recursive nature of the computer calculations, little differences would first cause tiny differences, which would
then affect the resulting next calculation a bit more, which would affect the output
of the next run even more. The final result of a long string of recursive
calculations would lead to complex diversity of geometric patterns (shapes).  Physics (physical form)
follows abstract mathematical function: Physics (physical form)
follows abstract mathematical function:
Is
there a connection between the Mandelbrot Fractal iterated
function (equation) of Z = Z squared
and
the many equations in physics that are squared?
"Could the reason why so many equations in physics are
squared represent aspects of a single truth based on just
one geometrical process?" what is significant is
that the inverse square law does not just apply
to Newton’s universal law of gravitation
it also applies to electric magnetic light"
[electricity, magnetism, light and heat].
Why is almost everything squared in physics?² E = Z, M = + C,
C2 = Z2 (laws of physics = fractal mathematics = physical form). - Newton's law of universal gravitation follows an inverse-square law, as do the effects of electric, magnetic, light, sound, and radiation phenomena. If you double the distance the light
intensity will be half. - A connection between fractal geometry
and physics (and biophysics, the application of the laws of physics to biological phenomena). A function is an equation that has only one answer for y for every x. A function assigns exactly one output to each input of a specified type.
 Mathematical infinity
a characteristic of the All-Person (Creator) and
fractals: There are an infinite (infinity) number of
decimal places in the number Phi (Golden Ratio a fractal scaling ratio). 1.61803398874989484820458683436563811772030917980576286213544862270526046281890
... In
a Logarithmic spiral there are an infinite number of revolutions, with the distance between them decreasing
as the curve approaches the center. Mandelbrot fractal set, for example, seemingly
infinite complexity is achieved with a very simple looking equation: Z = Z2 + C.
Pay special attention to the double arrow equal sign. This is very important because it signifies the recursive nature of fractals,
and the fact that there’s a built-in feedback loop. This
simple equation, given enough iterations, can produce patterns
that look as complex and as beautiful as the images... https://blog.kareldonk.com/the-holographic-and-fractal-universe/ 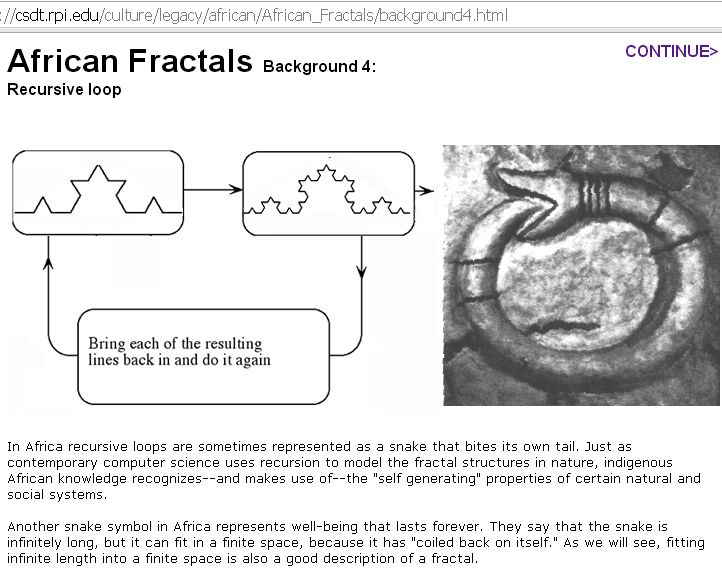 https://csdt.rpi.edu/culture/legacy/african/African_Fractals/background4.html https://csdt.rpi.edu/culture/legacy/african/African_Fractals/background4.htmlFractal geometry mathematics contains
the divine knowledge of Nature, the universe. and the Creator. In ancient times this divine knowledge was passed on to the
I'hins, then the Israelites and their close relatives in Africa and India, then
since the late 1970s modern man was inspired to discover fractals,
for this is the Kosmon cycle of universal knowledge (corporeal and spiritual)
and universal fellowship in all nations.  Kosmon, or,
Kosmon said. THE PRESENT ERA. All knowledge in possession of man, embracing Kosmon, or,
Kosmon said. THE PRESENT ERA. All knowledge in possession of man, embracing
corporeal and spiritual knowledge sufficiently proven. The Kosmon Bible is Oahspe. http://www.gailallen.com/rel/Oahspe/oah379.htm - Fractal
principles explain spiritual law and God and the Creator. Physical form follows mathematical function (computational code or
program). A fractal is created by recursion A + B = C (output), you take the output C and
bring it back in to repeat the process, where the output C becomes the
input C + A = D, then you repeat the process again, over and over. The output becomes the input which is KARMA, you get back what you put out, a spiritual
law which Walter Russell called rhythmic balanced interchange. Rhythmic means regular repetition or cyclic, balanced
means equal, interchange means giving and receiving or output and input. We Know we exist, so there is something in the universe that is self-similar to us but on a bigger or larger scale. The largest scale would
be the Infinite One, the All, the whole. The whole is in the part and
the part is in the whole (a fractal). Other spiritual teachings in the Bible that are
examples of recursion (iteration) where the output becomes the input: "Do to others as you
would have them do to you"- ◄ Luke 6:31 ► "Give, and it will be given to
you" - ◄ Luke 6:38 ► "and with what measure ye mete, it shall be measured
to you again" - ◄ Matthew 7:2 ► "for whatever a man sows, this he will also
reap" - ◄ Galatians 6:7 ► Recursion (iteration) is how a fractal is generated
or created. Proceedings of the Xxii World Congress of Philosophy 10:17-23 (2008). This research attempts to throw light on and show the fundamental similarities and differences between the African and Western ethical conceptions by examining the foundation of ethics and morality in
the two systems ... The African
indigenous ethics revolves round the “Golden Rule Principle” as the ultimate moral principle. The Africans’ which is more humanistic describes
morality and is better served. The main difference between the two ethical systems lies in the fact that whereas
the “golden rule” starts from the self and considers the consequences on the first before others, the universalizability
principle on the other hand considers the consequences on others
first before self. https://philpapers.org/rec/AZETGR https://www.pdcnet.org/wcp22/Proceedings-of-the-XXII-World-Congress-of-Philosophy Western culture,
sometimes equated with Western civilization, Occidental
culture, the Western world, Western society, and European civilization,
is a term used very broadly to refer to a heritage of social norms, ethical values, traditional customs, belief systems, political
systems and specific artifacts and technologies that have some origin or association with Europe. https://en.wikipedia.org/wiki/Western_culture A vortex with
logarithmic spirals (like a hurricane or spiral galaxy) is very fractal like. Logarithmic
spirals contain 4 essential components of fractal geometry. Logarithmic
spirals have recursion, scaling, self-similarity, and potential infinite
turns in the center. The universe is full
of recursive patterns &
self-similarity on all scales.  Above: images
of spiral galaxy and hurricane showing fractal self-similarity, scaling, and logarithmic spiral infinity.
“The
same flattening of the rotational curve is observed in the magnetohydrodynamics of stars and even hurricanes on earth,
both of which are vastly different in both scale and density. Finding self-similar characteristics in rotating
bodies across such enormous differences in
scale points to a common underlying mechanism.”
- OAHSPE BOOK OF COSMOGONY
IX:1 says "The same force, vortexya, pervadeth the entire
universe but different, according to volume, velocity and
CONFIGURATION. Page 17 of African Fractals by Ron Eglash: RECURSION...fractals are generated by a circular
process ... - Oahspe
Plate 47 - THE CYCLIC COIL: Jehovih...He is the circle without beginning or end... "Recursion is the motor of fractal geometry; it is here
that the basic transformations - whether numeric or spatial - are spun into whole cloth, and the patterns that emerge often tell the story of their whirling birth." - Page 109 of African Fractals. Definition
of whirl: to move in a circle ... Fractal recursive mathematics applies to physics, astronomy and other sciences. The Oahspe vortex unified field theory of the universe: Like a fractal a vortex is recursive, a circular process.
A vortex is sub-atomic particles (infinitesimal needles) in rotary (circular) motion. Magnetism
is a manifestation of a recursive vortex force.
Positive vortex'ya (vortex force) is the input of the vortex current. Gravity is the input of the vortex force. Negative vortex'ya (m'vortex'ya) is the output of the vortex current. When the
vortex force is charged or stored in iron or steel it is called magnetism. The current of the vortex force
is called electricity. When the vortex current causes the sub-atomic particles to line up in one direction it
is called light. When the stored up vortex force is liberated it is called fire or heat. A nuclear explosion is
liberated stored up atomic vortex force. Atomic mass is the manifestation of stored up vortex force. Chemical
elements are the manifestation of the velocity, pressure, configuration, and volume of the vortex force.  Above: vortex with currents and lines of force, output at bottom, input at top. Above: vortex with currents and lines of force, output at bottom, input at top.  Above left: magnet showing magnetic field lines (output N becomes input S) Above left: magnet showing magnetic field lines (output N becomes input S) Above center: vortex, output at bottom becomes input at top. Above right: solar system vortex, output at bottom past Neptune becomes input at top center or sun. Mathematical recursive vortex equation: A + B = C, next step or iteration of the recursive process = C + A or B = D. A + B = input, C = output, A + B = positive vortex'ya, C = negative or m'vortex'ya. The center of the vortex between the input and the output is neutral, corpor, atom, planet or sun. Above: blue line is positive vortex'ya, red
line is negative or m'vortex'ya. Oahspe Book of Cosmology
and Prophecy: Chapter I: 35. ..."the master's infinitesimal needles
remain poised from the sun centre outward, even to the earth, and may be compared to telegraph
wires"... = redline above. 15. The positive force of the vortex is, therefore, from the external toward the internal;
and the negative
force of the vortex is toward the poles, and in the ascendant toward the pole
external from the sun centre. Blue line above is input of the
circular recursive process, redline above is the output
of the circular recursive process. - Magnetic vortex - experimental proof.
The video linked here shows experimental proof of the existence of a magnetic vortex. The direction of rotation changes when magnetic polarity is reversed.
Usually, we see magnetic field lines shown as bending
straight back from one end of the magnet to the other. Correctly, what should
be shown is magnetic lines of force in a vortex configuration,
with flow spiraling into the Magnetic vortex spin proof:
Above is from page 142 of African Fractals by Ron Eglash, the Vodun god
Dan and periodic snake-like cycles notice how
very similar it is to the Oahspe concept of Dan, the Great Serpent and Cyclic
coil. In West Africa they call Dan the "cyclic Dan" and also "Dangbe",
this is very similar to Oahspe calling Dan a "cyclic dawn" and "synonymous with dang". See below for proof:   Me calling a "warm up-spike
year a time of Dan" is equivalent to the West African concept of "Regular phenomena in nature--the periodic aspects of weather ...are attributed to the action of Dan." Above we see from Oahspe the Roadway of the Solar Phalanx showing the snake-like great serpent of the solar system going through cyclic dawns of Dan. The Oahspe great
serpent and Dan (Dang) is very similar to the West African symbolic concept of Dan (Dangbe). Vodun cosmology centers around the vodun spirits and other elements of divine essence that govern the Earth, a hierarchy that range
in power from major deities governing the forces of nature and human society ... In West Africa Dan is pictured as "a
serpent biting its tail". In Oahspe Plate 48.--THE CYCLIC COIL you can
see the spiral currents of the
vortex spiral inward to the sun-center and then spiral and go out from the center toward the tail. Oahspe says "a
very long serpent in spiral form, constantly turning its head in at one pole, and its tail at the other". Above is an image of a recursive feedback loop, the output
at the bottom stage becomes the input at the top stage of cycle. If
one could imagine a very long serpent in spiral form, constantly turning its head in at one pole, and its tail at the other, and continuously crawling upon its own spirality, such a view would somewhat illustrate the currents of a vortex. - Book of Cosmogony and Prophecy Ch III: 25.  Above West African Dan (Dangbe) snake symbol swallowing his tail = mathematical iteration = cycle. Iteration, a dog chasing his tail or a snake swallowing it's tail
= the output at one end becomes the input at the other = the end of one cycle (arc of Bon)
= the beginning of the next cycle (Kosmon). Iteration = the
repetition of a process, or repetition of a mathematical or computational procedure applied
to the result of a previous application. -------------------------------------------------------------------------------------------------------------------------- The first attempt to model the distribution of galaxies with a fractal pattern was made by Luciano Pietronero and his team in 1987,[1] Pietronero argues that
the universe shows a definite fractal aspect over a fairly wide range of scale, https://en.wikipedia.org/wiki/Fractal_cosmology - …fractal patterns
exist at many scales in nature. Physicists believe that fractals
also exist in the quantum world, and now a group of researchers in the US
has shown that this is indeed the case. Quantum repetition, Fractal
patterns enter the quantum world.  This image shows the fractal pattern that results when the waves associated with electrons start to interfere
with each other. A fractal is a geometric entity whose basic patterns are repeated at ever decreasing sizes. Yazdani Lab: Visualizing Quantum States of Matter
(Princeton University, Department of Physics).  Above is quantum world image enlarged in square (original image just to the right upper). Notice the enlarged image (212%) is very similar to larger scale orange, green, and blue images in the original (100%). This shows self-similarity and scaling (on different size scales) of the quantum world. Mpc meaning in astronomy = A distance of one million parsecs is commonly
denoted by the megaparsec (Mpc). Astronomers typically express the
distances between neighbouring galaxies and galaxy clusters in megaparsecs. One parsec is equal to about 3.26 light-years (30 trillion km or 19 trillion miles) in length. Large scale distribution of galaxy clusters above shows a fractal pattern
very similar to neuron networks in the brain (like a Cosmic Consciousness). - "Mathematics is the language with which God wrote the Universe." – Galileo. Anything that can be measured is mathematics. Thoughts and Words are mathematics. Fractal Geometry is the mathematics in which the Creator wrote the Universe. - Michael James. In the beginning was the Word (mathematical concept) and the mathematical concept was with the Creator (Programmer) and the mathematical code was the Programmer (underlying recursive code that programed the universe of physical form).  Above: page 105 of Africa Counts by
Claudia Zaslavsky - Originally published: 1973 - Mathematics. 
Above and below is from pages 68-69 of African-Fractals by Ron Eglash. 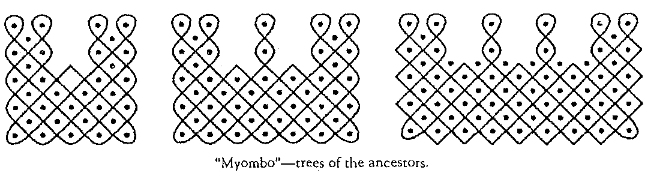 

Above Lusona drawings on T'Challa shirt in Marvel Black Panther movie. In graph
theory, an Eulerian trail (or Eulerian path)
is a trail in a finite graph which visits
every edge exactly once. https://en.wikipedia.org/wiki/Eulerian_path Will Hunting
solves a graph theory problem on a board in the hall posed by Professor Gerald Lambeau.  In the movie "Good Will Hunting" there is a particular mathematics problem in the movie: "Draw all homeomorphically irreducible trees of size n=10n=10." (ten valid trees). The rules • In
this case “trees” simply means graphs
with no cycles http://stanford.edu/class/archive/cs/cs106x/cs106x.1142/lectures/GoodWillHunting.pdf In mathematics,
and more specifically in graph theory, a tree
is an undirected graph in which any two vertices are connected by exactly
one path. In graph theory (mathematics) a
tree is a network of dots and lines (Numberphile Youtube). In mathematics, graph theory is the study of
graphs, which are mathematical structures used to model pairwise
relations between objects. A graph in this context is made up of vertices,
nodes, or points which are connected by edges, In
mathematics, graphs are useful in geometry and certain parts of topology such as knot theory. Algebraic graph theory has close links with group theory. https://en.wikipedia.org/wiki/Graph_theory  Above are Celtic
knots containing Eurlarian paths. Page 48 of African Fractals "...certain varieties of Celtic interlace designs. Nordenfalk
(1997) suggests that those are historically related to the spiral
designs of pre-Christian Celtic
religion,
where they trace the flow of a vital life force.
They are geometrically classified as an Eulerian path, which is closely
associated with mathematical knot theory (cf. Jones 1990, 99)."  https://en.wikipedia.org/wiki/Celts https://en.wikipedia.org/wiki/Celts
Migration map
of interlace knot designs and Eurlarian path knowledge from
Africa to Celtic Europe. Oahspe God's Book of Eskra 50:30-33: "Now,
after the fall of the great empire, Egupt, her
people migrated
westward, hundreds of thousands of them, and they settled
in western Uropa, where these people married with the aborigines.
Their offspring were called Druids, Picts, Gales (Gaelic), Wales (Welsh), Galls (Gauls),
and Yohans (Johns), all of which are Eguptian names, preserved to this day. " Interlace
knots and Eurlarian path knowledge predate the mathematician Leonhard Euler. Relating to the Celts or their languages, which constitute a branch of
the Indo-European family and include Irish, Scottish
Gaelic,
Welsh, Breton, Manx, Cornish, and several extinct pre-Roman languages such as Gaulish. https://en.oxforddictionaries.com/definition/celtic 
The plaited mat design in Figure 24 is well known from the central African cultural area. Among the Kuba
it is called ‘namba’, the bowels (Torday, p. 101). In
Kubik's view the 'sona' "transmit empirical mathematical
knowledge" (1987a, 450). The geometry of the 'sona' is a "non-euclidean geometry": "The forefathers of the Eastern Angolan peoples discovered higher mathematics and
a non-Euclidian geometry on an empirical basis applying their insights to the invention of these unique configurations" (Kubik,
1987b, 108). http://www.math.buffalo.edu/mad/Ancient-Africa/mad_angola-zambia.html Investigating the Mathematics of Sona: Sand Drawings from Angola. References [1] Paulus Gerdes, Drawings from
Angola: Living Mathematics, Morrisville, NC: Lulu.com,
2007. http://www.mathcircles.org/wp-content/uploads/2017/10/sona_lesson_0-1.pdf ...the Tchokwe [sona] drawing tradition, threatened with extinction during the colonial occupation... The sona tradition has been vanishing:
"What we find today is probably only the remnant, becoming more and more obsolete, of a once amazingly rich and varied repertoire of symbols" [Kubik, 1987, p. 59].
l
succeeded in reconstructing important mathematical elements of the sona tradition.
...probably
original sona have been reconstructed (cf. my analysis of the Tamil
drawing tradition in South India that
is technically related to the Tchokwe tradition. Gerdes [1989a]). 3. Educational and mathematical
potential Initially I was mostly interested in the reconstruction of the mathematical knowledge that had been present at the
invention of the sona. Many reported and reconstructed (sub)classes of Tchokwe ideograms
satisfy a common construction principle. By filming them starting the curve at one point, one sees a geometrical algorithm at work. The study of the mathematical properties of these curves constitutes a new and attractive research field. Possibly they may
be applied in the codification of information, in the development of laser memory circuits for optical computers, in the study of the topology of large scale
integration chips, etc. Probably the "akwa
kuta sona" who invented this and other construction rules [Gerdes, 1989c] knew why they were valid, i.e. they could prove in one way or another the truth of the theorems that these rules express.
On
the other hand, an analysis of Tchokwe sona stimulates the development of new mathematical research areas. http://webapp1.dlib.indiana.edu/virtual_disk_library/index.cgi/4273355/FID840/eqtyres/erg/111361/1361.htm  "not only in Angola, but also in other African countries, such as Ghana and the Congo,
many adults and children know immediately how many lines are needed – you only have to show them the array. When they see a rectangular array of points of dimensions 4 by 6, they quickly say that 2 lines are needed to
construct the lioness.
When you ask them how many lines are needed to encompass in
the same way all the points of an array of dimensions 5 by 7, they immediately
respond that one line will be enough." http://www.academia.edu/6922002/Drawnigs_From_Angola_-_Living_Mathematics   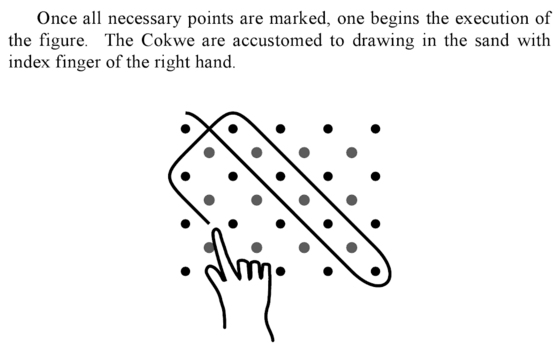 Oahspe The Lord's Fifth Book: Chapter VI:
29....and the seer sat therein, with a table before him, on which table sand was sprinkled. And the Lord wrote in the sand, with his finger, the laws of heaven and earth. ◄ John 8:6 ► of the Bible:
...Jesus stooped down, and with his finger wrote on the
ground,...  Above: Figure 10-3 page 106 of Africa
Counts by Claudia Zaslavsky.Africa Counts: Number and Pattern in African
Cultures
And
the Lord wrote in the sand, with his finger, the laws of heaven and earth. "the laws of heaven and earth" =
Algorithms = Binary fractal recursion (iteration), self-similarity, etc..
  "the
laws of heaven and earth" = Rules
of Prophecy = Cycles = recursion (iteration), self-similarity, etc..
...certain arithmetic or geometric "rhythms,"
called algorithms. - page 52 of Drawings
From Angola Living Mathematics, by Paulus Gerdes.
-
The Mathematics of Sona:Mathematical ideas
that readily appear include: • Graph Theory: what is a graph, Euler’s Formula. A particularly challenging question, which seems to have been investigated extensively, and experimentally,
by the Chokwe is "What layouts of dots, or dots and walls,
can give rise to one-line drawings, when following the "bouncing
ball" rule above?" Mathematicians investigating these
drawings have discovered a variety of theorems addressing parts of this question. The two most fundamental theorems discovered seem to have been known, in one
form or another, to the Chokwe artists. https://www.beloit.edu/computerscience/faculty/chavey/sona/ Network theory
origins in graph theory. Network theory was first introduce as “graph theory” by Euler. Rather
than “links” and “nodes” he called them
“vertices” and “edges.” Network theory origins in Lusona? Recall that lusona, the African design practice of drawing graphs in the sand, had exactly the same constraints: a connected
path that never re-traces. Could we also credit the Tchokwe with the origins of network theory? https://slideplayer.com/slide/7634412/  Figure 10-6 Kuba (Shongo) embroidered raffia cloth, Zaire (Congo). The interlacing mbolo pattern is similar to those drawn in the sand by Kuba children.
This cloth dates back to the eighteenth century. British Museum. - page 108 of Africa Counts: Number and Pattern in African Cultures by Claudia Zaslavsky - 1999 - Mathematics. eighteenth century
= The 18th century lasted from January 1, 1701 to December 31,
1800 in the Gregorian calendar. The cloth dates back to 18th century, the interlacing pattern concept dates back to before the 18th century in sub-Saharan Africa. In 1736 Euler solved, or
rather proved unsolvable, a problem known as the seven bridges of Königsberg.[8] The
city of Königsberg, Kingdom of Prussia (now Kaliningrad, Russia) is set on the Pregel River, and included
two large islands which were connected to each other and the mainland by seven bridges. The question is whether it is possible to walk with a route that crosses each bridge exactly once, and
return to the starting point. Euler's solution of the Königsberg bridge problem is considered to be the
first theorem of graph theory. https://en.wikipedia.org/wiki/Contributions_of_Leonhard_Euler_to_mathematics - Lusona is a Eulerian Path mandala [a geometric figure]
that shows up in the traditions of African and Indian cultures. https://www.pinterest.com/pin/564920346978377030/?lp=true The branch of mathematics that studies knots is known as knot theory, and has
many simple relations to graph theory. Perhaps surprisingly, there will always be some knotted loop in a sufficiently complicated network. Such “sufficiently complicated” networks are called intrinsically knotted graphs. Very complicated graphs are always intrinsically knotted, and very simple graphs
are always not, but graphs in between may be harder to identify.
When graph theory meets knot theory Joel
S. Foisy and Lewis D. Ludwig Abstract. Since the early 1980s,
graph theory
has been a favorite topic for undergraduate research due to its accessibility and breadth of applications. By the early 1990s, knot theory was recognized as another such area of mathematics,
in large part due to C. Adams’ text, The Knot Book. In this paper, we
discuss the intersection of these two fields and provide a survey of current
work in this area, much of which involved undergraduates. Application
of Graph Theory in real worldhttps://www.youtube.com/watch?v=7JlCfKLVEzs Chemical graph theory is
a branch of mathematics which combines graph theory and chemistry. Graph theory is used to mathematically
model molecules in order to gain insight into the physical properties of these chemical compounds. Some physical properties, such as the boiling
point, are related to the geometric structure of the compound. This is especially true in the case of chemical
compounds known as alkanes. Alkanes are organic compounds exclusively composed of
carbon and hydrogen atoms. The resulting representation of ethane is the carbon tree shown in Figure 2 . This carbon
tree can be represented as a graph by replacing
the carbon atoms with vertices. Chemical bonds are then
represented as an edge in the graph. https://www.maa.org/external_archive/joma/Volume8/Burch/Research.html 
Above rotating model of the diamond cubic crystal structure. More images for diamond molecular model. Above diamond (crystal carbon) molecular
model is a network of dots and lines made up of vertices, nodes, or points which are connected
by edges. --- There
are many useful applications to Euler circuits and paths. In mathematics, networks can be used to solve many
difficult
problems, like the Konigsberg Bridge problem. They can also be used to by mail carriers who want to have a route where they don't retrace any of their previous steps. Euler circuits and paths
are also useful to painters, garbage collectors, airplane pilots and all world navigators, like you! http://www.geom.uiuc.edu/~doty/applications.html Applications of
Graph Theory in Everyday Life and Technology About Moses below:  doctrine
of one Great Spirit, Whom they worshipped secretly under the name Jehovih. Moses
rebuilt what had been lost since Abraham's time. Lost to African-Americans since
the time of Christianity, slavery, and Islam in Sub-Saharan Africa is the
traditional belief in the Great Spirit and the
mathematical knowledge of fractal geometry, I would like for both to be rebuilt and shared
with the rest of the world. - New prophets arise in Kosmon (since 1848): Oahspe Book of
Sethantes Chapter 9: 16. The Lord said: And yet further on, a brighter light
adorneth the way: Great Jehovih's hand sendeth the traveling worlds into
the light of kosmon, and new prophets arise gathering up the histories lost,
and glorious plan of the Great Spirit over all. - We need to break the shackles of Christianity and the Constantine Bible.   https://news.brown.edu/articles/2016/01/shackles https://news.brown.edu/articles/2016/01/shackles Slavery Timeline
1400-1500. 1441 1441: Start of European slave trading in Africa.
The Portuguese captains Antão Gonçalves and Nuno Tristão
capture 12 Africans in Cabo Branco (modern Mauritania)
and take them to Portugal as slaves. 1444 8 August 1444: de Freitas lands 235 kidnapped and enslaved Africans in Lagos, the
first large group of African slaves brought to Europe.
1452 18 June
1452: Pope Nicholas V issues Dum Diversas, a bull authorising
the Portuguese to reduce any non-Christians to the status of slaves. 1454 1483 1483: Diogo Cão discovers the Congo
river. The region is later a major source of slaves. 8
January 1454: Pope Nicholas V issues Romanus Pontifex, a bull granting the Portuguese a perpetual monopoly in trade with Africa. Nevertheless, Spanish traders begin to bring slaves from Africa to Spain.
1500 22
April 1500: Pedro Cabral of Portugal discovers Brazil, landing at Porto Seguro, southern Bahia. http://www.brycchancarey.com/slavery/chrono2.htm Slavery
Timeline 1501-1600. 1502
1502: Juan de Córdoba of Seville becomes the first merchant we can identify
to send an African slave to the New World. Córdoba,
like other merchants, is permitted by the Spanish authorities to send only one slave. Others send two or three. 1509
1509: Columbus's
son, Diego Cólon, becomes governor of the
new Spanish empire in the Carribean. He soon complains that Native American slaves do not work hard enough.
1510 22
January 1510: the start of the systematic transportation of
African slaves to the New World: King Ferdinand of
Spain authorises a shipment of 50 African slaves to be sent to Santo Domingo. 1518 18 August 1518: in a significant escalation of the slave trade, Charles V grants his Flemish
courtier Lorenzo de Gorrevod permission to import 4000 African slaves into New Spain. From this point onwards thousands of slaves are sent to the New World each year.
http://www.brycchancarey.com/slavery/chrono3.htm 1518 to 2018 = 500 years. Both the knowledge
and the slave labour of the Israelites were now thus impressed into the construction of the temple of Osiris, the Great Pyramid. And the etherean dawn in which Moses would bring them deliverance was still five hundred years away.[2053
- 500 = 1553 B.C.E.]. - Pages 189-190 of Darkness, Dawn And Destiny (Drawn
from Oahspe) 1965 by Augustine Cahill. 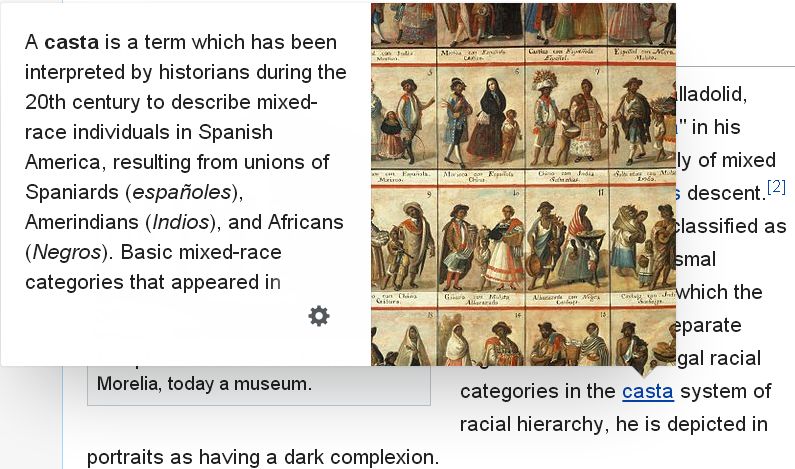 ...the baptismal register,[3] a system
in which the Catholic Church kept separate registers for different legal
racial categories in the casta system of racial hierarchy, https://en.wikipedia.org/wiki/Jos%C3%A9_Mar%C3%ADa_Morelos Spain practiced the Indo-European caste system.  Spanish Casta = Caste, breed, race (see above Google translate). Spanish Casta = Caste, breed, race (see above Google translate). Above image shows the hierarchy of the
Spanish Indo-European CASTA (caste) system, with enslaved Africans at the bottom. The Criollo (Spanish pronunciation: [ˈkɾjoʎo]) are Latin Americans who are of full or near full Spanish descent, distinguishing them from both multi-racial Latin Americans and Latin Americans of post-colonial
(and not necessarily Spanish) European immigrant origin. Historically,
they were a social class in the hierarchy of the overseas colonies established by Spain beginning in the 16th century, especially in Hispanic America, comprising the locally born people of Spanish ancestry.[1] Although Criollos were legally Spaniards, in practice, they ranked below the Iberian-born Peninsulares. Nevertheless, they had preeminence over
all the other populations: Amerindians, enslaved Africans and peoples of mixed descent. According to the
Casta system, a criollo could have up to 1/8
(one great-grandparent or equivalent) Amerindian ancestry without losing social place (see Limpieza de sangre).[2] https://en.wikipedia.org/wiki/Criollo_people The Spanish along with the Portuguese were heavily involved in the African slave trade. Because slaves
were shackled on the slave ships their only had to be about 30 spanish crew-men on the ship for every 300 slaves. Middle Passage - Wikipedia Slavery - BBC World Service | The Story of Africa And because the trans-atlantic trip from Europe to the Caribbean was perilous
(dangerous) the spanish men kept their wives and girlfriends home in Spain (example; in the 1700s departing from the ports of Belfast or Derry, these "hardy middle-class farmers and craftsmen" made the eight-week-long voyage across the oftentimes storm-tossed North Atlantic,
see Confucius, Po, China, Jaffeth & Caucasian origin & destiny page of this website about
2/3 down from top), and because of this the population of New Spain in Mexico which stretched from South-America to Canada (with
Mexico city as the capitol) at first was more Africans than there was Spanish, with the Indigenous Native American Indians
being the highest population. Men being men when they became sexually aroused who did they have sex with? Their spanish women
were in Spain. Since they only had Native American and African women to choose from, that is who the spanish men had sex with,
and that is how Mullatoes and Mestizos were born in Mexico. Later after cities and government was established the spanish
men sent for their women in Spain and transported them to the New World (New Spain - Mexico) and the Spanish and European
population increased. After slavery was abolished in Mexico after they won independence from Spain (in 1810), African slaves
were not brought over to Mexico anymore and the Spanish and European immigration continued. During the next 200 years the
black population of Mexico was more and more diluted. According to the 1570 spanish census of Mexico the black population
of Mexico was higher than the European and Spanish population of Mexico, and their was more Mulattos (half-black-half-european)
than their was Mestizos (half-Native American-half-european). According to the 1646 Spanish census of Mexico their was more
Mestizos than any other population in Mexico except for the American Indians, but their was still more blacks than spanish
or europeans. In 1742 their was still more blacks in Mexico than Spanish or europeans. It was until the 1793 census that spanish
and europeans outnumbered blacks in Mexico. https://blog.diegovalle.net/2016/01/afro-mexicans.html This is why today when Mexicans or Mexican-Americans take a DNA test, it reveals to many (that
are surprised) that they have 6 or 7 percent African DNA in them, and in some cases as much as 9 or 11 percent African DNA
in them. Puerto-Ricans are more knowledgable about their black African ancestry and they know they have about 30% African
DNA in them. The Racial Integrity Act was subject to the Pocahontas Clause (or Pocahontas Exception),
which allowed people with claims of less than 1/16th American
Indian ancestry to still be considered white, despite the otherwise unyielding climate of one-drop rule politics.[8][9] ---------------------------------------------------------------------------
The original religion of the African people, however, was animism (the worship of spirits), and there is no doubt that most of the slaves were
animists. http://web.archive.org/web/20160622194754/http://www.raceandhistory.com/cgi-bin/forum/webbbs_config.pl?md=read;id=2307 an·i·mism animism
2. the belief in a supernatural power that organizes and animates the material universe.
https://www.google.com/#q=animism+definition "a supernatural power that organizes and animates the material universe"
= The Great Spirit (Jehovih).
Shamanism is the practice that involves a shaman reaching
an altered state of consciousness in order to meet up with and interact with the spirit world and channel mystical and supernatural energies
into this world, or this reality.
Shamanism shares the animistic worldview that non-human entities such as animals, plants, and
inanimate
objects or phenomena, all possess a spiritual essence or soul. Shamanism also shares the animistic belief in a supernatural power that organizes
and animates the material
universe, namely – The Great Spirit or God. http://web.archive.org/web/20170418092404/http://www.takuwakan.com/shamanism/ Some Common Lakota
Words and Terms. Taku Wakan: Wakan Relatives. (“Relatives” relates to all things in nature, not just to blood relatives or other
humans.) http://sdpb.sd.gov/oceti/documents/LakotatermsTable.pdf Oahspe God's First Book: Chapter XXVII: 42. From far over the
water will I bring their kindred (Jews)[Israelites], who worship
none born of woman; a wise speaking people.
A people that war not; who kill not off weaker nations. American Indians and Africans before slavery were shamanists and animists and believed in the Great Spirit. Oahspe Book of Jehovih Chapter I: 2.
He said, I Am! And He comprehended all things, the seen and the unseen. Nor is there aught in all the universe but what is part of Him. 3. He said, I am the soul of all; and the all that is seen is of My person
and My body. The Message of The Divine
Iliad, By WALTER RUSSEL: “For behold,
said the Universal One, I am within all things centering them". Testimony from the Bible and Thomas Paine and Oahspe:
The Bible: 1 Chronicles 4:40:
English Standard Version
"where they
found rich, good pasture, and the land was very
broad, quiet, and peaceful,
for the former
inhabitants there belonged to Ham."
-
"The Managers of that Trade themselves, and others, testify,
that many of these African nations
inhabit fertile countries, are industrious farmers, enjoy plenty,
and lived quietly, averse to
war, before the Europeans
debauched them with liquors, and bribing them against one another; and that these
inoffensive people are brought into slavery, by stealing them, tempting Kings to sell subjects, which they can have no right to do, and hiring one
tribe to war against another, in
order to catch prisoners." - African Slavery in America by Thomas Paine (1775). Oahspe The Lord's Fifth Book: Chapter
III:
13. The Lord said: Having designed Ham for teaching
the barbarian world of me and my dominion, Ham (son of Noah) - Wikipedia -  The Babylonian geometric patterns in stone above show two-fold and four-fold symmetry (up/down, left/right),
they are NOT fractal. Above is Clay panel with pattern of squares
and triangles - Ishtar Gate from Babylon - Pergamon museum
in Berlin, Germany. 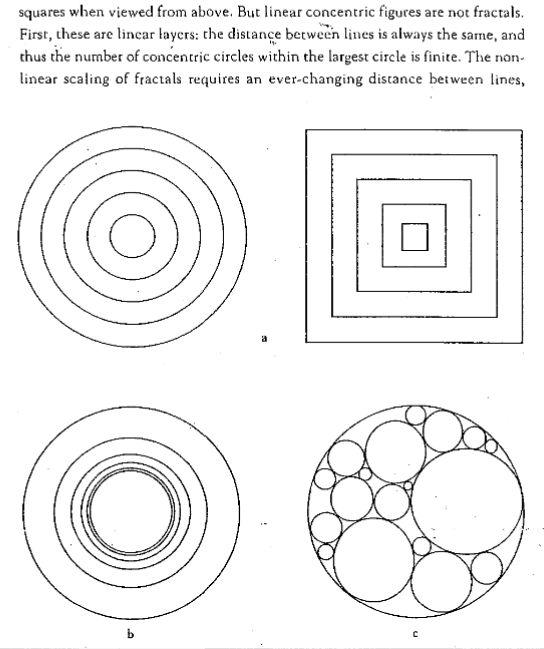  "...like concentric squares when viewd from above but linear concentric figures are not fractals...
The non-linear scaling of fractals requires an ever-changing distance between lines,
which means there can be an infinite number in a finite space."
- Pages 41-42 of African Fractals. - Fractals, Complexity, and Connectivity in Africa.
Page 102...a year of fieldwork in West
and Central Africa involving interviews with the artisans provide convincing evidence that they
are better classified as intentional, conscious designs: that something analogous to fractal construction
techniques – recursive scaling practices – exists as an African indigenous knowledge
system. page 106...an
understanding of African mathematical representations, fractals,
complexity and chaos in indigenous cultural practices ... https://homepages.rpi.edu/~eglash/eglash.dir/afractal/Eglash_Odumosu.pdf
"...a portrait of mathematical sophistication in non state societies creates a strong conflict with the old ladder model of cultural evolution, a model that is itself
overdue for extinction." - Page 190 (at bottom) of African Fractals by Ron Eglash. ...In stateless societies, there is little
concentration of authority; most positions of authority that do exist are very limited in power ... While stateless societies were the norm in human
prehistory, few stateless societies exist today; ... https://en.wikipedia.org/wiki/Stateless_society From :59 to 1:23 the word Hebrew means "those who have passed from place to place", similar to Nomad or wanderer.
https://www.youtube.com/watch?v=_mPWsRGPpY0 From 4:47 to 6:01 of above video (DECODING THE HEBREW ISRAELITES WITH OAHSPE): Oahspe Book of Eskra chapter 10 verse 10-11 "And so great was the spiritual power of the Oralites, that
during all these hundreds of years the Faithists, six millions, had lived without king or governor. Being as a multitude of communities." Type of societies 1000 BC (below). Purple = Nomadic like the Hebrew Israelites (Saharan-Sahel-Horn of Africa and Arabian pastoral nomads) = Arabinya
of Oahspe. "This
bottom-up, or self-organized, plan contrasts with a top-down, or hierarchical, plan in which only a few people decide
where all the houses will go." - Ron Eglash, African Fractals. "One
difference between a stateless and state-based society is that the
governance in the former evolves from the bottom up, primarily through voluntary agreements, while governance
in the later involves top-down coercive command."
http://www.freenation.org/a/f33b1.html Stateless
nomadic society = Ancient Hebrew Israelites of Africa and Arabia.   The letters ARABIN are written across the African countries of Mali, Niger, Chad,
and Sudan. The letters YA are written across the Arabian Peninsula nation of Saudi
Arabia. A connection
between traditional mathematical (fractal) sophistication and Nomadic pastoral non state societies and ARABINYA of OAHSPE and the Hebrew Isrealites. Above Arabin'ya map of Oahspe. Arabinya = Arabian peninsula
and Africa. Oahspe Book
of Cpenta-Armij, Daughter of Jehovih: Chapter IV: 11. ...In Arabin'ya I have raised up a man
named Abram, an I'huan of the I'hin side, of grade ninety-five. http://web.archive.org/web/20130515174413/http://www.sacred-texts.com/oah/oah/oah229.htm Oahspe
First Book of God Chapter 11: 23.
Now when Abraham and his people came into Arabin'ya,
especially into Egupt, ... when
Oahspe refers to Arabin'ya, it includes a large area of land which covers all or part of Africa and what is now the Middle East to Iran. http://oahspestandardedition.com/OSAC/WhowasThoth.html "...an indigenous, continent-wide belief system among African people stands at the very root of
Hebrew culture
..." - HEBREWISMS OF WEST AFRICA, by Joseph J. Williams. ----------------------------------------------------------------------------- Using Sierpinski fractal to analyze and investigate
pore distribution and heat transfer performance of metal foam. Effect
of Pore Distribution on Melting Behavior of Paraffin in Fractal Metal Foam* An unsteady model of melting heat transfer in metal foam filled with paraffin is developed and numerically
analyzed. In the model, the pore distribution of metal foam is described by Sierpinski fractal. By this fractal
description, six types of metal foams with the identical porosity,
different pore distributions are reconstructed. The effect of pores distribution on the heat transfer performance of the
paraffin/copper foam composite is emphatically investigated. The solid-liquid distribution, the evolution of the
melting front, the dynamic temperature response and the total
melting time in these six fractal structures are all examined and analyzed. The results indicate that, the pores distribution
has a significant impact on the melting heat transfer of the paraffin in the metal foam. When
the first-level fractal pore is located near the heat source boundary, the thermal hysteresis effect of the paraffin on the solid matrix heat transfer is more significant. If the cross-sectional
length of the pores along the normal direction of heat transfer
is larger, the heat transfer barrier of the solid matrix is
greater. It is favorable for the paraffin heat transfer when the pores specific surface area is larger. http://iopscience.iop.org/article/10.1088/0253-6102/70/4/501 realm (left), shown in an image indicating the density
of electrons on the surface of copper. Physicists have
created an oddity known as a quantum fractal, a structure that
could reveal new and strange types of electron behaviors. Electrons inhabiting a fractal don’t live in 3-D like the rest of us. Nor do they exist in a flat 2-D
world or a one-dimensional line. Instead they occupy an in-between,
fractional number of dimensions. In this case, the scientists
found that the electrons lived in approximately the number of dimensions expected for a Sierpinski triangle, 1.58. Quantum particles
tend to act in unusual ways when confined to one or two dimensions (SN: 10/20/16, p.6). Scientists don’t yet know how electrons
will behave in fractional dimensions, says physicist Cristiane Morais Smith of Utrecht University in the Netherlands.
“What can come out of our work is completely uncharted territory.” NOVEMBER
12, 2018. https://www.sciencenews.org/article/physicists-wrangled-electrons-quantum-fractal Scientists Trapped Electrons In a Quantum Fractal (And It's Wild!) https://www.youtube.com/watch?v=OsZHRCuTIS8 ---------------------------------------------------------------------------------------------------------- Volume 98, January 2019, Pages 74-79 Compact microstrip antenna based on fractal metasurface with low radar cross section and wide
bandwidth. The compact antenna with wide bandwidth
is important. In this paper, we have studied the microstrip slot antenna
for wireless application based on the fractal structure which has covered 2.3–4?GHz (85% bandwidth). The fractal model
has been considered for low RCS, for improving the bandwidth, for amending the matching of the antenna by controlling the current distribution and it is modified for C-band application. The results show that the
fractal shape is used for the bandwidth enhancement and experimental results are confirmed by our simulations. As a result, we show that how the metasurface combination with the antenna
can be considered for improving the bandwidth and RCS simultaneously. The microstrip antenna
is a conventional kind of antenna for radar application which it is used
for various applications such as communication system, medical application, mobile services and radar systems in missile
[1], [2].In addition, the radar cross section (RCS) of the antenna is known as an important factor for some of these applications [3]. The radar cross section (RCS) is noticed for stealth application
by coating the surface of an aircraft [4], [5]. Exactly, the RCS is a parameter for measuring of the object detection and the low RCS means that an object can find hard [hard to find] by radar systems. Consequently,
it is attractive for stealth application [6]. On the other hand, nowadays antennas with low RCS have been
noticed while the fractal technique is one of the main methods for this goal [7]. Moreover, the ultra-wideband antenna with low RCS has been
considered such Vivaldi antenna [8], the monopole antenna with small ground [9]. Furthermore,
as mentioned the fractal method is developed as a conventional
method for RCS reduction while the fractal shapes are known as self-similar shapes, and are usually found in galaxies,
cloud boundaries, mountain ranges, coastlines, snowflakes, trees, and leaves [13] and fractal method have been examined for various applications like antenna [14] and the absorbers based on metamaterial [15]. Recently, the fractal shapes are more attractive to reflect-array
[16], [17], [18] and monopole [18] antenna to reduce the RCS.  Fig. 1. The four steps in antenna design from slot antenna to slot antenna with the fractal ring. Fig. 1. The four steps in antenna design from slot antenna to slot antenna with the fractal ring. Fig. 2. The antenna’s geometry (a) the ground layer with parasitic elements, (b) the feed line geometry
and (c) the fabricated antenna. 4. Conclusion The slot antenna is known as
best antenna in various applications like radar
systems and on the other hand low RCS and wide bandwidth are
both necessary for these systems and so the slot antenna with
fractal formation and parasitic element is suggested for C-band application. https://www.sciencedirect.com/science/article/pii/S1434841118306538 ----------------------------------------------------------------------------- Studies of Nonlinear Phenomena in Life Science: Volume
1 Fractal Physiology and Chaos in Medicine. This book discusses the
application of the concepts of fractals and chaos to biomedical phenomena. In particular, it argues against the outdated notion of homeostasis;
using biomedical data sets and modern mathematical
concepts, the author attempts to convince the reader that life is at least a homeodynamic process with multiple states — each being capable of survival. https://worldscientific.com/worldscibooks/10.1142/1025 ------------------------------------------------------------------------------ What can a snowflake teach us about how cancer spreads in the body? What can seashells, lightning and the coastline of Britain teach us about new drugs
for cancer? The
answer, according to a team of researchers at the USC Viterbi School of Engineering, may revolve around fractals, the infinitely complex patterns found in nature. In this case, fractals can also help describe how the control of insulin expression signals blood glucose regulation or how something as duplicitous as cancer spreads in the body and the right tools
to stop it. Conventional math cannot adequately model the interaction of multiple genes over multiple time frames—a necessary foundation for
any cancer-fighting drugs. https://medicalxpress.com/news/2018-12-snowflake-cancer-body.html --------------------------------------------------------------------------------------------------------------- The splendid generative potential of the Sierpinski triangle  December 14, 2018, The Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences
One transistor can become an oscillator
with a surprising richness of behavior. However, even more interesting
effects
emerge if the structure of connections is fractal and shows some imperfections. Could similar rules explain
the diversity and complexity of human brain dynamics? Intuition suggests that self-similarity appears only in systems as complex as neural networks in the brain, or in fascinating shapes of nature, for example, in fractal Romanesco broccoli buds. At the Institute of Nuclear Physics of the Polish
Academy of Sciences (IFJ PAN) in Cracow, researchers made a discovery that in some ways challenges this belief. In close collaboration with colleagues from the University of Catania and the University of
Trento in Italy, the researchers constructed an elementary electronic oscillator based on just one transistor. As it turns out,
when it contains fractal arrangements of inductors and capacitors, these
generate amazingly rich characteristics of the electrical signals. Scientists from all disciplines have long been fascinated by fractals.
But it is only recently that engineers have started taking an interest in them for practical applications.
The latest research shows that in
simple, fractal electronic oscillators, imperfections in the structure of connections radically increase the dynamics of behavior. This result
provokes some speculations related to the structure and functions of the human brain. "We might be tempted to assume that imperfections in the layout of neural connections
arise accidentally in a process of brain growth from a structure
that would otherwise be ideal by definition. In fact, this is probably not the case, and their presence may serve a specific purpose and be a result of long-term natural selection.
Neural networks with defects will manifest more complex
dynamics. Who knows, then, if inspired by this observation, one day we will even intentionally build imperfect computers?"
sums up Prof. Drozdz. https://phys.org/news/2018-12-splendid-potential-sierpinski-triangle.html ------------------------------------------------------------------------------------------------------------- Scientists demonstrate fractal light from lasers Date: January 30, 2019 Source: University
of the Witwatersrand Reporting this month in Physical Review
A, the team provide the first experimental evidence for fractal
light from simple lasers and add a new prediction, that the fractal light should exist in 3D and not just 2D as previously thought. Fractals are complex objects with a "pattern within a pattern" so that the structure appears to repeat as you zoom in or out of it. Nature creates such "patterns
within patterns" by many recursions of a simple rule, for example, to produce a snowflake. Computer programmes have also been used to do so by looping through the rule over and over, famously producing the
abstract Mandelbrot Set. The light inside lasers also does this: it cycles back and forth, bouncing between the mirrors on each pass, which can
be set to image the light into itself on each round trip. This looks just like a recursive loop, repeating a simple rule over
and over. The imaging means that each time
the light returns to the image plane it is a smaller (or bigger) version
of what it was: a pattern within a pattern within a pattern. Fractals
have found applications in imaging, networks, antennas and even medicine. The team expect that the discovery of fractal forms
of light that can be engineered directly from a laser should open new applications and technologies based on these exotic states of structured light.  Above: A cross section of a fractal pattern, created by a laser in the Wits Structured Light Laboratory. Wits Structured Light Laboratory in
Johannesburg, South Africa: ------------------------------------------------------------------------------- Recently, scientists realized that many
of the natural and biological phenomenon or objects in nature can be explained in the most appropriate way by introducing fractals rather than using the conventional Euclidean representations [19].
In the present article it is intended to analyze the significance of fractals
in bio-nanosystems which can contribute new information
to the scientific community and also opens a new area
of possibility in research
in the field of fractal applications. “We will see that the gaps are not one-sided: just as Africans were missing
certain mathematical ideas [such as fractional dimension] in their version of
fractal geometry, Europeans were equally affected by their own cultural views and have
been slow to adopt some of the mathematical concepts [such as recursion] that were long championed by Africans.” African Fractals - Scribd 
https://3010tangents.wordpress.com/2015/03/02/history-development-and-applications-of-fractal-geometry/ ...fractal geometry has also found diverse applications in fields such as structural
engineering, medicine, telecommunications, urban
planning, and more.[viii] Iterative methods have been used to create high-strength construction cables
by interweaving a series of thinner wires into thicker ones that, in turn, are used in the next iteration to make
even larger and stronger cables than before. This simple procedure, usually no more than a few iterations for most industrial purposes,
bears a resemblance
to a fractal
pattern and allows us to make use of the special properties that fractal geometry offers.
- Any comments about Oahspe or this website? Email Me. I look forward to talking to you about Oahspe and this website.
free HitCounter
|
|